16

In his book The Signal and the Noise, Nate Silver presents this example application of Bayes's Theorem on pp. 247-248:

Consider a somber example: the September 11 attacks. Most of us would have assigned almost no probability to terrorists crashing planes into buildings in Manhattan when we woke up that morning. But we recognized that a terror attack was an obvious possibility once the first plane hit the World Trade Center. And we had no doubt we were being attacked once the second tower was hit. Bayes's theorem can replicate this result.

You can view the complete example in Amazon.com's previw, and I've made the two pages available here.

Silver assumes the prior probability of a terrorist plane attack to be 1 in 20,000. After the first plane crash, using Bayes's Theorem he updates that to 38%. And after the second plane crash, he comes up with a 99.99% probability. However, I think he may be mistaken. I'll provide the details below.

To be precise, let us define the following three events:

  • $PC$ = Plane Crash: At least one plane crashes into a Manhattan skyscraper on a given day.
  • $TPA$ = Terrorist Plane Attack: At least one plane is intentionally crashed into a Manhattan skyscraper on a given day.
  • $APC$ = Accidental Plane Crash: At least one plane is accidentally crashed into a Manhattan skyscraper on a given day.

We assume all plane crashes into buildings are either terrorist plane attacks or accidental (i.e. $PC = TPA \cup APC$). Using historical data, Silver estimates the prior probability of an accidental plane crash to be 1 in 12,500. In summary: $$P(TPA) = \frac{1}{20000},$$$$P(APC) = \frac{1}{12500}.$$

Furthermore, Silver assumes $P(APC) = P(PC|\overline{TPA})$ (which is true if $APC$ and $TPA$ are independent events).

Applying Bayes's Theorem, he comes up with $$\begin{align}P(TPA|PC) &= \frac{P(PC|TPA) \times P(TPA)}{P(PC|TPA) \times P(TPA) + P(PC|\overline{TPA})(1-P(TPA))} \\ &= \frac{1 \times \frac{1}{20000}}{1 \times \frac{1}{20000} + \frac{1}{12500} \times (1 - \frac{1}{20000})} = 0.385\end{align}$$

Silver continues:

The idea behind Bayes's theorem, however, is not that we update our probability estimates just once. Instead, we do so continuously as new evidence presents itself to us. Thus our posterior probability of a terror attack after the first plane hit, 38 percent, becomes our prior probability before the second one did. And if you go through the calculation again, to reflect the second plane hitting the World Trade Center, the probability that we were under attack becomes a near-certainty -- 99.99 percent.

That is (this is Silver's calculation): $$P(TPA|PC) = \frac{1 \times 0.385}{1 \times 0.385 + \frac{1}{12500}(1-0.385)} = 99.99 \%$$

"Cool!" I thought, until I thought a bit more. The problem is that you can apply the same logic to calculate the conditional probability of an accidental crash, too. I'll spare you the math, but I come up with $P(APC|PC) = 0.615$ after the first crash, and $P(APC|PC) = 99.997\%$ after the second.

So we can be almost certain the second plane crash is a terrorist attack, and we can be even more certain that it's accidental?

I think the problem is that when Silver applies Bayes's Theorem after the second crash, he uses the updated probability of a terrorist plane attack as his prior, but fails to update the prior probability of an accidental plane crash (which should become 0.615). After the second crash, then, the correct formula is $$P(TPA|PC) = \frac{1 \times 0.385}{1 \times 0.385 + 0.615(1-0.385)} = 0.504$$

Similarly, the probability that we're observing an accidental crash given that there have been two crashes is $$P(APC|PC) = \frac{1 \times 0.615}{1 \times 0.615 + 0.385(1-0.615)} = 0.806$$

Question 1: Am I correct that Nate Silver is doing it wrong?

Question 2: Am I doing it right?

David
  • 604
  • It seems like this reasoning could be applied to anything - if you flip your null hypothesis you're likely to get a different result. – Cocopuffs Jan 04 '13 at 04:14
  • You computed the conditional probability of something being true on some observations, then you computed the conditional probability that it's false on the same observations, and the two probabilities don't add up to $1$. So that's bad. – Qiaochu Yuan Jan 04 '13 at 04:21
  • When you apply Bayes' theorem the second time, you need to be clearer about what your hypotheses are. A priori there are four hypotheses depending on which of the two planes was an accidental crash vs. a terrorist crash, and if one of the planes was a terrorist crash it's much more likely that the second one is too, so you need to take that into account. – Qiaochu Yuan Jan 04 '13 at 04:23
  • Qiaochu: Regarding the first comment, APC and TPA aren't disjoint (mutually exclusive) when there have been 2 or more crashes, so the probabilities need not add up to 1. There is merit to your second comment. But the problem is that after the first plane crash, we don't know whether it was a terrorist attack or an accident. All we know is that a plane has crashed into a building. Later on, all we know is that two planes have crashed into buildings. The question after each crash is: how likely is it that a terrorist attack has occurred. – David Jan 04 '13 at 04:30
  • One problem here is that the chance of an accidental crash remains small, while we are not given any information about 2-plane terrorist attacks - but while the probability an accidental crash remains plausibly independent of the past, this is not true in the case of a second terrorist attack. – Mark Bennet Jan 04 '13 at 04:31
  • 1
    Incidentally, an example to show the mathematics involved in Bayes to a non-specialist - assuming a UK population of 60,000,000. Lawyer gets up in court and presents forensic evidence which proves that the match between the accused and the criminal is one in a million - which sounds convincing. However, this means there are 60 people in the population who would match the forensics and our accused is just one of those 60. Unless we have more evidence we can't say the accused is the criminal. – Mark Bennet Jan 04 '13 at 04:36
  • @Mark Bennet, the correct figure is one in a million, for DNA or other forensic evidence of the kind gathered independently of, and subsequent to, the arrest of the suspect. It is ten times higher if there are initially 10 suspects and only the one with matching DNA is brought to trial, but this is still a very small probability of getting the wrong man. – zyx Jan 08 '13 at 23:51
  • @zyx I did say "unless we have more evidence". There are two probabilities - first the probability that a random man from the population fits the forensics, which is indeed 1 in a million - this goes to show how difficult it is to find one of the small number who do fit the profile by a process of random (or even systematic) testing. The second is the probability that the particular man in front of us is the criminal. There are 60 possibilities in the population, and there is certainly no reason why a process of random testing should locate the right person as the first fit to the profile. – Mark Bennet Jan 09 '13 at 07:29
  • @MarkBennet, the non-forensic criteria single out one subset of the population containing, let us say $n$ individuals (the suspects based on proximity in space and time, testimony from witnesses and other basic police criteria) who are then DNA tested. There is another subset, the 60 individuals who fit the DNA profile. To a very reasonable approximation these two sets are independent of each other, so the probability that they intersect is about $n$ in a million. Either we have the criminal or an incredible coincidence has taken place. – zyx Jan 09 '13 at 14:09
  • @zyx I have excluded other factors "non-forensic criteria" - I'm not doing 'real world' but 'simple model'. Note, though, that genetic factors can be localised within regions, families or population groups - whic would also provide a bias in the sample. – Mark Bennet Jan 09 '13 at 14:17
  • The lawyer in your example is not arguing about the one-subset "simple model" (being in a 1 per million subpopulation of 60 million people = 1 of 60) but the question of why the two small subsets intersect. The one-subset argument is much less typical of what is actually argued at court. It can arise in situations where a suspect is apprehended and then the authorities go fishing for characteristics that can support a prosecution. But this is more difficult to do with forensic evidence like DNA that is generated separately from the arrest process. (@MarkBennet) – zyx Jan 09 '13 at 21:39
  • @zyx The lawyer in my example is as much a part of the model as the other bits - a figment of my imagination, if you like. – Mark Bennet Jan 09 '13 at 23:02
  • One thing comes to my mind. What about time? What if both events occurred within a wider time span, let's assume a year? It seems plausible to me that a second attack is very likely an act of terror within a view hours, but what about months or years? What means "second event" in this case? – Jürgen R. Plasser Jul 06 '13 at 11:31

5 Answers5

2

So we can be almost certain the second plane crash is a terrorist attack, and we can be even more certain that it's accidental?

Correct, there is no contradiction here.

If we know that the first crash was a terrorist attack, then the second crash would be more likely another terrorist attack.

The same reasoning with accidental crashes.

Question 1: Am I correct that Nate Silver is doing it wrong? Question 2: Am I doing it right?

No. There is no need to update the rate of accidental crashes. IMHO, Nate implies that accidental crashes don't include terrorist ones. Otherwise, he couldn't multiply probabilities in the denominator.

Mike
  • 21
  • "If we know that the first crash was a terrorist attack" .. but we don't know that. All we know is that there was a first crash. Knowing this, the probability that the first crash was a terrorist attack is not 100%. It's 38%. And the probability that we have just experienced an accidental crash is 61.5%. – David Jan 04 '13 at 13:59
2

though the chance of two accidental plane crashes can multiplied to give you a very small number (1/12500 x 1/12500) since they are independent, one cannot assume the same for a terrorist attack. Once we think that the first plane crash is a TPA, it would not make sense to assume that the second crash, if it is also a TPA, to be independent and not highly correlated (perhaps 90% chance that the 2nd plane crash is TPA given the first is TPA) to the first. so if you use 1/20000 x 0.9 to get the probability that both plane crashes are TPA, you will not end up with the problem you mentioned that both scenarios have become more likely.

user55281
  • 21
0

I think Nate did a bad job explaining his thinking. For me Bayes is confusing, so I try to make it very clear what my assumptions are to explain the probabilities.

In his example, his initial probability (.005%) describes the likely-hood of terrorist attacks in Manhattan via plane attack into skyscrapers prior to 9/11. This means 99.995% of the time is not a terrorist attacks in Manhattan via plane attack, which is NOT just accidental plane crashes. It would be everything including normal days with no crashes and accidental plane crashes.

He then uses plane crashes as a test on these two events. He doesn't explicitly say this, but his test is to assume every plane crash is a terrorist attack. Given there is a terrorist attack to hit a Manhattan building with a plane, we are 100% that our test, a plane crash, will tell us so.

On the flip side, the 99.995% side, what are the chances our test, plane crashes are terrorist attacks, accurately predicts no terrorist attack? Well, accidental plane crashes into Manhattan buildings have shown a historical precedence of .008% likely-hood to occur. This number is a false positive for our test, the chance a plane crash incorrectly predicts there was a terrorist attack. This can also be understood as the chance our test will say it was a terrorist attack given it was a normal day OR an accidental plane crash .

I made a diagram:

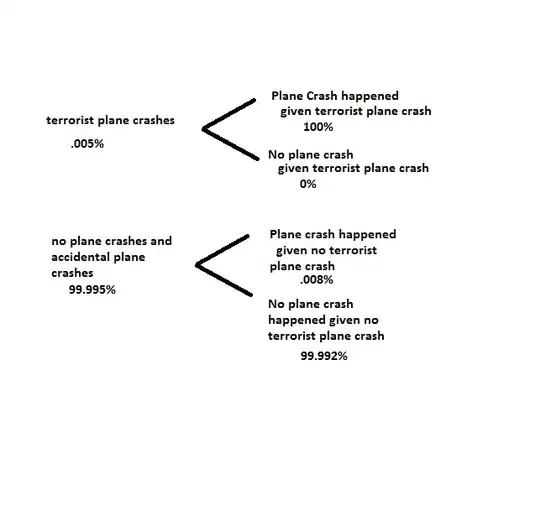Chart Using Bayes, you can establish what is the likely-hood there was a terrorist attack in Manahattan via plane crash given that a plane crashed, using your plane crash test.

You can run this model to get the updated value of an accidental plane crash AND normal days given a plane crash as you've done as well (61.5%). As you may have noticed, 100% - 38.5% = 61.5%. Essentially, this is the OPPOSITE of Nate's assumption, and the number isn't going up, its going down from 99.995%. This model is agnostic to whether the plane crash was a terrorist attack or an accident, as some of the above answers are confused about. This model already takes into the account the likely-hood of accidents and terrorist attacks with its plane crash test.

61.5% does NOT fit into the false positive plane crash test slot as that would change your model. 61.5% is the likely-hood that there was an accidental plane crash given there was a plane crash, NOT the probability of a plane crash given that it's not a terrorist attack via plane crash. You don't change the .008% the same way Nate didn't change the 100% when updating his formula the second round of Bayes because the equation already takes it into account. The second round of Bayes assumes you have no new information on whether the plane crash was a terrorist attack or an accident.

I believe your main concern is Nate makes an assumption that the first plane was a terrorist attack for the second plane attack. He does not. This Bayes inference simply tells us the likely-hood of plane crashes being terrorists attacks given that there were plane crashes. The only "assumption" Nate made was there were two plane crashes. Given two plane crashes using this model, your likely hood of it being an accidental plane crash AND a normal day becomes .00128%, it does not go up as you've mentioned and it does not describe JUST accidental plane crashes but both accidental plane crashes AND normal days.

Hope this helps!

user3662796
  • 1
0

P(TPA_1/PC)=0.38 P(TPA_2/TPA_1)=0.9 (if 1st plane crash is TPA, 2nd plane crash is almost surely TPA since the two events are highly correlated) P(APC_1/PC)=0.62 P(APC_2/APC_1)=1/12500 (on a bright sunny day, accidental plane crashes have to be independent of each other) hence probability that it is a terrorist attack when the 2nd plane crashed= P(TPC_2/TPC_1)P(TPC_1/PC)/ (P(TPC_2/TPC_1) P(TPC1/PC) + P(APC_2/APC_1) P(APC_1/PC) ) = (0.9 X 0.38)/(0.9X0.38+ 0.62X 1/125000)=99%

user55281
  • 21
0

I think there is a misunderstanding of Bayes' theorem here. When you update the probability, you do so because you know for sure what has happened the first time; you are not guessing. In the example, Nate Silver assumes, after the first crash, that it was terrorist caused. With that assumption, you go and update and get a new probability. So, the meaning of the 99.9% is that "IF" the first crash was terrorist caused, then there is almost certainty that if there is a 2nd one, it will also be terrorist caused. Now, if the first was accidental, and later there is a second one, you can also be almost certain that the 2nd was another accident.

nachobit
  • 1