0

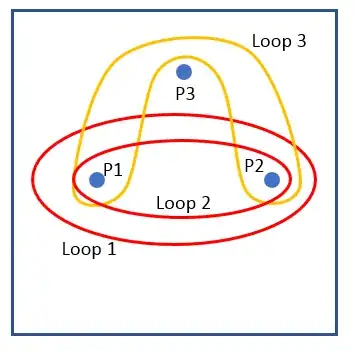
A plane removes several points, for example, here P1, P2, P3. Loop 1 and Loop 2 are freely homotopic(or called homotopic if have same base point). Loops 3 are not homotopic with loop 1 and 2, but it also encircle point P1 and P2, like loop 1 and loop 2. Is there a specific name for this kind of loops (here loop 1 and loop3) that encircle same points?

enter image description here

Qi Zhong
  • 153
  • 1
    You also need orientation on your loops. Then such loops are called homologous. – Moishe Kohan Mar 05 '18 at 01:52
  • @MoisheCohen Thank you. Yes, it will take the orientation into consideration. It seems the word "homologous" is correct, I am looking for references which I can understand about this topic. – Qi Zhong Mar 05 '18 at 02:39
  • Any textbook on algebraic topology will cover both fundamental group, homology groups and relation between them (Hurewicz theorem). https://math.stackexchange.com/questions/84409/best-algebraic-topology-book-alternative-to-allen-hatcher-free-book. My favorite reference is Massey's book. – Moishe Kohan Mar 05 '18 at 05:48
  • Now I can understand "There are only two kinds of math books: Those you cannot read beyond the first sentence, and those you cannot read beyond the first page." by Chen-Ning Yang. As a graduate in physics, I find math books are not written for us(ordinary people or students/researchers not in math major). Of course this is because math is precise and restrict to be written in this way. – Qi Zhong Mar 05 '18 at 16:20
  • Did you try "Topology for physicists" by Albert Schwartz? It does cover the basics of algebraic topology. – Moishe Kohan Mar 05 '18 at 16:38
  • See also suggestions at https://www.google.com/url?sa=t&source=web&rct=j&url=https://physics.stackexchange.com/questions/29956/book-covering-differential-geometry-and-topology-for-physics&ved=2ahUKEwiI08nTztXZAhUX84MKHQG3B-AQjjgwFXoECAkQAQ&usg=AOvVaw1zIH4TXRfsppcuPAr3nRIv – Moishe Kohan Mar 05 '18 at 18:05
  • Thank you so much. I will take a look at these books. – Qi Zhong Mar 05 '18 at 18:07
  • Let us continue this discussion in chat. – Qi Zhong Mar 05 '18 at 23:33

0 Answers0