I'm interested in finding the following constant:
$$b=\sum_{n=1}^\infty \left(\frac{1}{a_n}-\frac{1}{(n+1) \ln (n+1)} \right)$$
Where:
$$a_1=2$$
$$a_{n+1}=a_n+\log a_n$$
This is related to my recent question where the sequence was first introduced and it was shown in the answer that:
$$\lim_{n \to \infty} \frac{a_n}{n \ln n}=1$$
I wanted to see what the constant above looks like, because this is similar to how the Euler-Mascheroni constant is obtained from the harmonic series and the logarithm.
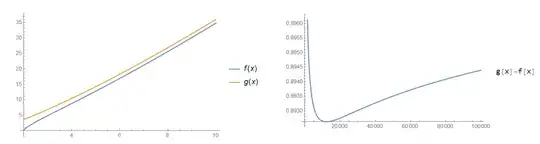
The problem is, the convergence of the above series is extremely slow. And I mean so slow, that I'm not even sure what the first digit is.
From Mathematica computations it seems that:
$$0.1 <b <0.2$$
But I'm only sure about the upper bound, because $b$ becomes smaller as the number of terms increases.
Note that even though initial partial sums are negative, $b$ becomes positive soon, because the sequence $a_n$ gets overtaken by $(n+1) \ln (n+1)$, even if they are of the same order. You can see that in the linked question.
Then $a_n$ overtakes $(n+1) \ln (n+1)$ again, and partial sums start to decrease.
Mathematica gives:
$$\sum_{n=1}^{10^7} \left(\frac{1}{a_n}-\frac{1}{(n+1) \ln (n+1)} \right)=0.18702446577 \dots$$
But at least the second digit is different from the true value of $b$, as can be seen by adding further terms.
$$\sum_{n=1}^{10^8} \left(\frac{1}{a_n}-\frac{1}{(n+1) \ln (n+1)} \right)=0.1738163796928 \dots$$
(In case it's important, I was keeping only $100$ digits of each $a_n$ while computing the recurrence terms. Maybe there's some loss of precision there as well).
Update
$$\sum_{n=1}^{10^9} \left(\frac{1}{a_n}-\frac{1}{(n+1) \ln (n+1)} \right)=0.162 \dots$$
(I have more digits, but it's clear they don't matter at this point).
And for some $10^9<N<10^{10}$ (aborted computation) we have:
$$b<0.1599565$$
Can we find at least a few first digits of $b$? What methods would you suggest for accelerating the series or transforming it somehow for faster convergence?
The motivation for this question is not the sequence itself (I don't believe it has any significance) but rather methods for solving this kind of problems.
As a side question, can we at least prove that the series converges? I'm rather convinced it does, but just in case.
For other series related to the sequence we have, reliably:
$$\sum_{n=1}^\infty \frac{1}{a_n^2}=0.57409540\dots$$
$$\sum_{n=1}^\infty \frac{(-1)^{n+1}}{a_n}=0.285408\dots$$
The convergence is quite slow for these cases as well, which was expected by comparison with known series.