I came across this painting(http://www.galleriarusso.com/works/10586-pythagorean-theorem.html) which clearly shows a dissection proof of the pythagorean theorem. The closest proof I found was #72 on this page. I have two questions. 1) Would someone be kind enough to walk me through a proof of the #72 diagramm on the above page and 2) Can anyone suggest a proof based on the dissection in the painting. Thanks in advance!
Asked
Active
Viewed 191 times
2 Answers
4
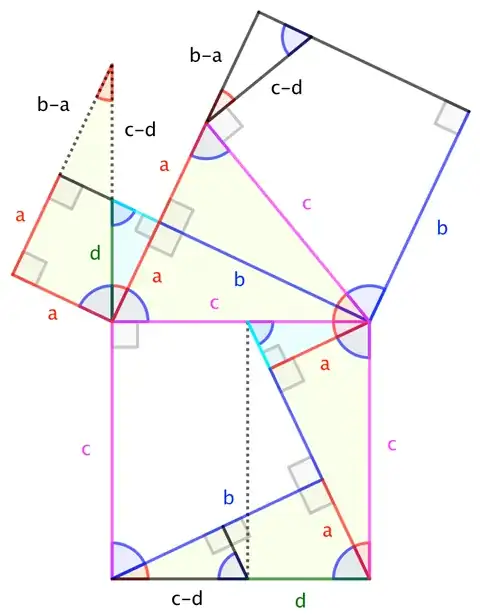
As @DavidQuinn notes, the appearance of the black equilateral triangle forces the right triangle to be $30^\circ$-$60^\circ$-$90^\circ$. However, as @G.Sassatelli notes, the "orange+green+black" subdivisions aren't actually relevant to the dissection, since those elements are treated as a fixed grouping.
If we ignore the black equilateral triangle, and merge the "orange+green+black" into a single quadrilateral region, then the dissection ---which applies to arbitrary right triangles, so long as $a$ is the shorter leg--- can be understood by observing multiple appearances of the $a$-$b$-$c$ triangle throughout the figure. Labeling various edge-lengths should make this pretty clear:
As for proof of Cut-the-Knot's #72 ... I'll have to come back to that.
Blue
- 83,939
-
thanks so much! excellent diagram, much clearer now. I'm guessing the odd splitting of the parallelogram was more artistic license than anything else. – JZachary Feb 24 '18 at 06:50
1
It would seem that this is not intended to be a general "proof without words" of the Pythagorean theorem. This is because the pink triangle is intended to be congruent to the original triangle and the black triangle is intended to be equilateral, meaning that the original triangle and the pink triangle together comprise an equilateral triangle.
So the original triangle is in this case half an equilateral triangle and not a general right angled triangle..
David Quinn
- 35,087