0

Problem Statement :

An industrious father called his only one son and told that he had bought gold by his whole life income and put this gold in the jungle . His son asked the position of gold in the jungle .

So father told that there were two similar tress named A and B in the jungle . Also there was a stone named S . To find gold son had to follow the following instructions .

After reaching A from S, he can get the point C perpendicular and equal to the distance SA . Again , he could go to B from S and get the point D after walking perpendicular and equal to the distance SB .

Now the son could find the gold in the midpoint of CD . The son had found the point A and B but could not get the point S .

Can the son get the gold ? If he can , then how ?

My trying :

I have tried to understand/solve the problem after drawing geometric figure . But I got stuck and could not get out of this .

So I want help . Please help me .

Sultan Ahmed
  • 531
  • 1
    No, you need to know whether to make a right turn or a left turn after walking from S to A to find C. (and S to B to find D) – Doug M Dec 28 '17 at 05:38
  • But the son has not found the point S. So how can I decide to left turn or right turn ? – Sultan Ahmed Dec 28 '17 at 05:40
  • 1
    Assume you know where S is, and draw the figure. Then try $S_2$ and draw the figure. If x marks the same spot for both figures, then know the starting point is irrelevant. If it doesn't then you are probably out of luck. – Doug M Dec 28 '17 at 05:43
  • Can you explain this with necessary figure ? – Sultan Ahmed Dec 28 '17 at 05:47
  • I think the problem also needs to specify which way you turn when you reach A (or B) going from S, in order to reach C (or D), and for one of the two it needs to be clockwise and for the other - anticlockwise. Then, it will turn out that the midpoint of CD does not depend at all of S so the son can pick any point as S. The proof I've seen uses complex numbers (let A be -1, let B be 1, let S be z, calculate C and D and their midpoint and it turns out to be i (or -i, depending on the direction in which the son turns at A and B)). Please try to fill in the gaps. –  Dec 28 '17 at 05:48
  • One way to proceed: If the gold could be found from any starting place $S$, then you could choose a convenient place for $S$ and see where the gold must be. (There are four possibilities depending on your choice of left or right turns. I see you've provided in a comment that you have specific turns. That narrows the choice of points to one.) Then, prove that the gold's location remains fixed as $S$ changes. – Blue Dec 28 '17 at 06:07
  • 1
    This problem and relatives show up here every so often. See https://math.stackexchange.com/a/2076585/265466, https://math.stackexchange.com/q/2276768/265466, https://math.stackexchange.com/q/2312508/265466, &c. – amd Dec 28 '17 at 08:11

3 Answers3

2

I think that this is easiest to solve using complex analysis.

If we say A, B, S are at arbitrary points in the complex plane.

The journey from $A$ to $S$ can be represented as $S + (A-S)$ And a vector that is $90^\circ$ perpendicular of equal length and a right turn is $-i(A-S)$

And then we do something similar for the vectors from $S$ to $B$ to $D.$ However a left turn is $i(B-S)$

$x =S + \frac 12 ((A-S) - i(A-S)) + \frac 12((B-S) + i(B-S)) = \frac 12 A + \frac 12 B + \frac 12 i(B-A)$

And $x$ does not depend on $S$ and can be found by $A,B$ alone

To find the treasure, start at A. Walk half way to B, turn left $90^\circ$ walk and equal distance as you covered to the halfway point. Dig.

Here is a figure, not quite to scale.

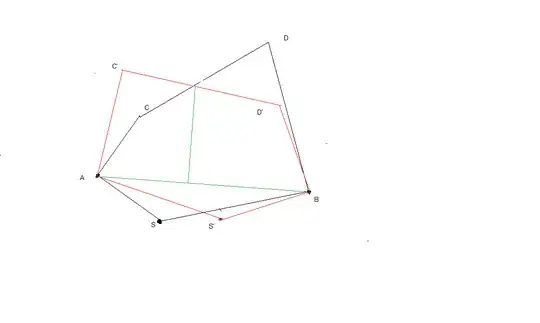
enter image description here

Doug M
  • 58,694
1

Following up on my comment...

Assuming we additionally specify that the son needs to turn right by $90^\circ $ at $A $, and left by $90^\circ $ at $B$, here is a solution that I remembered, using complex numbers.

Let us set the origin and the axes so that $ A $ is at $-1$, $B $ is at $1$. Let $S $ be at $z $. Then, $\vec {AS}=z+1$, $\vec {AC}=i (z+1) $ and so $C=i (z+1)-1$. Similarly, $\vec {BS}=z-1$, $\vec {BD}=-i (z-1) $ and $D=-i (z-1)+1$. Now, the midpoint $G $ (gold) of $CD $ is given as $G=\frac {1}{2}(C+D)=\frac {1}{2}(i(z+1)-1-i (z-1)+1)=\frac {1}{2}\times 2i=i$. In other words, find the location of the imaginary number $i $ - the gold is there.

(Note this does not depend on $z $ (i.e. on S) and so the son can also find gold by following instructions while taking any $S $ he wants.)

1

Let's draw a map. We can choose any orientation and scale we want.

so let $A$ be $(0,0)$ and $B$ be $(0,1)$. Let $S$ be $(u,v)$. We don't know what those are.

The distance from $S$ to $A$ is $\sqrt{u^2 + v^2}$. The slope of $SA$ is $\frac vu$. (We'll have to make a special exception if $u=0$). And the equation for line $AS$ is $y = \frac vu*x$. The slope of $AC$ is therefore $-\frac 1{\frac vu} = -\frac uv$ (We'll have to make a special exception if $v = 0$) and the formula for $AC$ is $y= -\frac uv*x$.

So if the point $C = (a,-\frac uva)$ then the distance for $AC$ is $\sqrt{a^2 + \frac {u^2}{v^2}a^2} =|a|\sqrt{1 + \frac{u^2}{v^2}} = \sqrt{u^2 + v^2} = |v|\sqrt{1 + \frac {u^2}{v^2}}$ so $|a| = |v|$ and $C= (\pm v, \mp u)$.

The distance for $S$ to $B$ is $\sqrt{u^2 + (v-1)^2}$. The slope of $SB$ is $\frac {v-1}u$ so the slope of $BD$ is $-\frac {u}{v - 1}$ (again, special exception if $v = 1$). The equation of line $BD$ is $y = -\frac u{v-1}x + 1$.

So if the point $D = (b, -\frac u{v-1}b + 1)$ then the distance from $BD$ is $\sqrt{b^2 + (-\frac u{v-1}b)^2}=$$|b|\sqrt{1 + \frac {u^2}{(v-1)^2}} $$= \sqrt{u^2 + (v-1)^2} = |v-1|\sqrt{1 + \frac{u^2}{(v-1)^2}}$

So $|b| = |v-1|$ so $b = \pm v \mp 1$ and $D=(\pm v\pm 1, \mp u + 1)$

So there are four possible possible positions for the gold. They are:

$(\frac {v+v+1}2, \frac {-u-u + 1}2) = (v + \frac 12, -u + \frac 12)$. We're screwed. We'll never find it. We curse our father and wonder why he couldn't have simple told us whether we have to turn left or right at points $A$ and $B$. If we turn right at $A$ and right at $B$ we'll never find it.

$(\frac {v - v - 1}2, \frac {u-u + 1}2) = (-\frac 12,\frac 12)$. We dig there and hope our father meant we turn right at $A$ and left at $B$.

$(\frac {-v + v + 1}2, \frac {-u+u + 1}2) = (\frac 12,\frac 12)$. We dig there and hope our father meant we turn left at $A$ and right at $B$.

$(\frac {-v-v-1}2, \frac {u+u + 1}2) = (-v - \frac 12, u + \frac 12)$. We're screwed. We'll never find it. We curse our father and wonder why he couldn't have simple told us whether we have to turn left or right at points $A$ and $B$. If we turn left at $A$ and left at $B$ we'll never find it.

fleablood
  • 130,341