1

A sinusoid is an interesting shape (understatement of the day)..

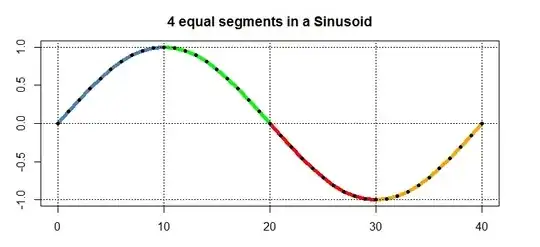
In the image below you see a sinusoid with period 40 and amplitude 1 (the image scale is incorrect). It consists of 4 identical segments: if you reflect the first, blue segment about the vertical line x=10 , you get the green segment, which you then reflect about the X-axis, and about the vertical line x=20: it returns the red segment, which after a reflection about the vertical line x=30 returns the yellow segment: enter image description here

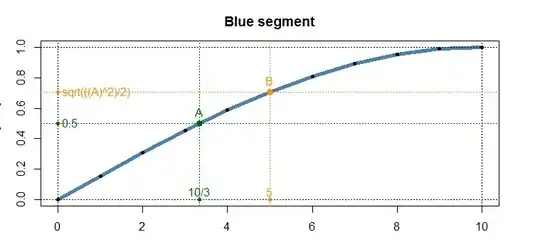
Now if you focus on 1 of these 4 identical segments, i.e. the first, blue one: there are 2 interesting points on the blue curve: the green point A and orange point B: I refer to the image below: enter image description here

  • Point A: is the green dot on the blue curve: the point where the horizontal line of y=0.5 (half the Amplitude of the sinusoid) intersects with the sine curve. It can be seen that the X-axis coordinate of this intersection point is at 1/3rd the length of the segment. Remember that 1 segment is 1/4th the total wave's period. 1/3rd of 1/4th is 1/12th the period. In plain English: half the height of the segment is covered by one third its length, and the next half of the height requires two thirds of the segment. So there is structure in the deceleration of the ascent of the curve.

  • Point B: is the orange point on the blue curve: the point where the vertical line of x=5 (half the length of the segment) intersects with the sine curve. It can be calculated that the Y-axis coordinate of the intersection point with the sinusoid and the vertical line at half the segment length, is at sqrt(((A)^2)/2) of the amplitude. In plain English: after you pass half the length of the segment, you will increase in height by a factor of the square root of half the squared amplitude.

These 2 points: half the height for 1/3rd the length, and half the length for sqrt(((A)^2)/2) the height (with A = the amplitude).

This is true for any period / amplitude, and I have not seen this documented anywhere.

Do you know of any other interesting geometric properties of sinusoids that are interesting or less commonly known? Maybe at other pi/.. points of the segment? Or other multiples of the amplitude (i.e. 0.25 or 0.75)?

Thanks!

MisterH
  • 357
  • 2
    So ... $$\sin\left(\frac13\text{ of }\frac{1}{4}\text{ of period}\right)=\frac12\text{ of amplitude} \qquad\leftrightarrow\qquad\sin 30^\circ = \frac12$$ $$\sin\left(\frac12\text{ of }\frac14\text{ of period}\right) = \frac{1}{\sqrt{2}}\text{ of amplitude} \qquad\leftrightarrow\qquad\sin 45^\circ = \frac{1}{\sqrt{2}}$$ I'm pretty sure this kind of thing is documented somewhere. – Blue Dec 16 '17 at 17:00

2 Answers2

2

The four segments are no surprise. You are just inheriting the symmetry of the circle.

The second property is more interesting: the are very few values for which a rational multiple of the period yields a rational value. This constitutes Niven's theorem (https://en.wikipedia.org/wiki/Niven%27s_theorem).

The third property is a simple consequence of Pythagoras' theorem in a rectangle isoceles triangle, the hypothenuses of which is $\propto\sqrt{1^2+1^2}$.

Sorry to say, but these properties are pretty anecdotic.

  • Thanks Yves, I was interested in this "four segments" property, because of these 2 previous related questions. It is also related to a property of the WMA & EMA filters: you can create a causal, in-phase filter of equal frequency (without lag) by taking the difference of these 2 filters if you calculate them over a window of p/4. – MisterH Dec 23 '17 at 14:54
0

This is true for any period / amplitude

No magic there. Say you have a period $P$ and an amplitude $A$. Then your curve is defined as

$$y = f(x) = \sin\left(x\cdot\frac{360°}{P}\right)\cdot A$$

So if you observe $f(a\cdot P)=b\cdot A$ for some numbers $a,b$ (like $a=\frac14\cdot\frac13=\frac1{12},b=\frac12$ for your point $A$ or $a=\frac14\cdot\frac12=\frac18,b=\frac1{\sqrt2}$ for your point $B$ noting $\sqrt{\frac{A^2}2}=\frac1{\sqrt2}\cdot A$) you are essentially observing $\sin(a\cdot 360°)=b$ which is independent of the period and amplitude.

So what you observe is essentially

$$\sin\left(\frac{360°}{4\cdot3}\right)=\sin\left(30°\right)=\sin\left(\frac\pi6\right)=\frac12\\ \sin\left(\frac{360°}{4\cdot2}\right)=\sin\left(45°\right)=\sin\left(\frac\pi4\right)=\frac1{\sqrt2}$$

I have not seen this documented anywhere

I'm sure now that you've seen a different way to write this, you'll find plenty of occurrences. For example the section on special values in the Wikipedia article on Sine and the image Wikipedia uses in that article:

Unit circle angles

Do you know of any other interesting geometric properties of sinusoids that are interesting or less commonly known? Maybe at other pi/.. points of the segment?

The Wikipedia article Trigonometric constants expressed in real radicals has a long list for other specific angles. But I would not consider most of them terribly exciting.

Of course it sepends on the task at hand. For example in my answer to Is there a way to draw a 1 degree angle using only ruler and compass? I spent a lot of time on $\cos(40°)=\sin(50°)$, not because it had any nice and easy value, but to the contrary because its value was surprisingly complicated.

In everiday practice I'd remember $\sin60°=\frac{\sqrt3}2$ in addition to those you have. Personally I prefer to remember these special values as

$$\sin0°=\frac{\sqrt0}2\quad\sin30°=\frac{\sqrt1}2\quad\sin45°=\frac{\sqrt2}2\quad \sin60°=\frac{\sqrt3}2\quad \sin90°=\frac{\sqrt4}2$$

Parts of the curve other than the blue can be derived from this, as can the cosine curve.

Or other multiples of the amplitude (i.e. 0.25 or 0.75)?

In my experience, the arc sine of a simple fraction tends to be a transcendental number in most cases, so writing these down as anything else than $\arccos\left(\frac14\right)$ is usually none too useful.

MvG
  • 44,006