1

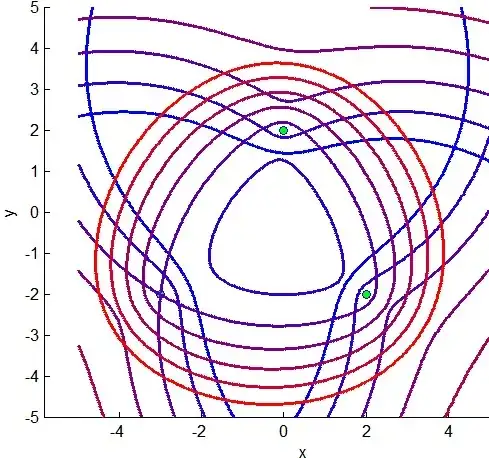
I am looking for n-ellipse parametric equation. n-ellipse is an equidistant curve from n foci.

https://en.wikipedia.org/wiki/N-ellipse

The implicit equation is provided in the document:

http://math.ucsd.edu/~njw/PUBLICPAPERS/kellipse_imaproc_toappear.pdf

The Theorem 2.1.

And also just would like to share my maple code for this (3 points):

interface(rtablesize = 20)

with(LinearAlgebra)

M := proc (u, v) options operator, arrow; Matrix(2, 2, [[x-u, y-v], [y-v, -x+u]]) end proc

M1 := M(u1, v1)

M2 := M(u2, v2)

M3 := M(u3, v3)

I2 := IdentityMatrix(2, 2)

U8 := KroneckerProduct(KroneckerProduct(M1, I2), I2)+KroneckerProduct(KroneckerProduct(I2, M2), I2)+KroneckerProduct(KroneckerProduct(I2, I2), M3)

D8 := K*IdentityMatrix(8, 8)

H8 := D8+U8

So the result for this particular 3-point case is:

Matrix(8, 8, [[K+3*x-u1-u2-u3, y-v3, y-v2, 0, y-v1, 0, 0, 0], [y-v3, K+x-u1-u2+u3, 0, y-v2, 0, y-v1, 0, 0], [y-v2, 0, K-u1+u2+x-u3, y-v3, 0, 0, y-v1, 0], [0, y-v2, y-v3, K-u1+u2-x+u3, 0, 0, 0, y-v1], [y-v1, 0, 0, 0, K+u1-u2+x-u3, y-v3, y-v2, 0], [0, y-v1, 0, 0, y-v3, K+u1-u2-x+u3, 0, y-v2], [0, 0, y-v1, 0, y-v2, 0, K-x+u1+u2-u3, y-v3], [0, 0, 0, y-v1, 0, y-v2, y-v3, K-3*x+u1+u2+u3]])

DSkoog
  • 325
Gevorg Hmayakyan
  • 2,036
  • 1
    Thanks for attracting our attention to this interesting paper. Your question concerning a parametric representation of an n-ellipse can find an answer in (https://math.stackexchange.com/q/3329) (using the y=mx "trick" for example) – Jean Marie Nov 30 '17 at 12:33

1 Answers1

1

This is not an answer, but a complement ; it can bring a supplementary light about these analytical expressions for ''eierkurven" which, surprinsingly, are expressible using Kronecker sums and products.

As in your example, $K$ is the sum of distances to the 3 fixed points $A_1, A_2, A_3$.

You will find here two figures:

  • First figure : $A_1(0,0), A_2(0,3), A_3(4,0)$ (forming a right triangle) $K=7$ in blue, $K=8$ in red.

Please note that the small loops alone constitute the loci : the remaining parts of the curves, similar to borromean rings cannot be separated in a direct way.

Please note also that curve $C_7$ (corresponding to $K=7$) passes through $A_1$ and curve $C_8$ passes through $A_2$.

See Matlab code, very similar to yours, at the bottom.

enter image description here

  • Second figure : $A_1(-3,-2), A_2(2,-2), A_3(0,2).$ From $K=8$ (closed blue curve) to $K=14$ (closed red curve). The other branches are not part of the loci enter image description here

Matlab program for the first figure (I include it because a certain number of SE users work with this environment) :

 clear all;close all;hold on;
 a=13;axis([-a,a,-a,a]);axis equal
 syms x y
 u1=0;v1=0;u2=0;v2=3;u3=4;v3=0;
 plot([u1,u2,u3],[v1,v2,v3],'o','MarkerFaceColor','g','MarkerSize',6);
 M=@(u,v)([x y ; y -x]-[u v ; v -u]);
 I=eye(2);M1=M(u1,v1);M2=M(u2,v2);M3=M(u3,v3);
 U1=kron(kron(M1,I),I)+kron(kron(I,M2),I)+kron(kron(I,I),M3);
 for K=7:8
    U=U1+K*eye(8);
    g=ezplot(['',det(U),''],[-a,a,-a,a]);set(g,'color',[K-7,0,8-K]);
 end;

Remark: A certain parallel (no intended pun) can be made with the so-called "offset curves", as can be found for example in (https://documat.unirioja.es/descarga/articulo/3217873.pdf), a typical example being that a second degree curve such as an ellipse has a parallel curve which is as well with degree 8 !

Jean Marie
  • 88,997