Assume there is a unit disk with radius = 1 and centered at $C$. Randomly and uniformly pick a point $P$ in the disk. What is the expected distance between $C$ and $P$?
Solution:
Since $P$ is $\bf{Uniformly Distributed}$, we know the probability is $\frac{1}{\pi}$, use polar coordinates substitution $x = r\cos{\theta}$ and $y = r\sin{\theta}$, we know
$E[\sqrt{x^2+y^2}] = \frac{1}{\pi}\int_{0}^{2\pi}\int_0^1r*rdrd\theta = \frac{2}{3} $
Here is the problem. How do we generate a uniformly randomly distributed $P$ in real life?
At my original thinking, there are two independent variables, $\theta$ and $r$, every point in the disk can be represented by these two variables. Thus, we uniformly pick an angle from $[0, 2\pi)$ and distance from $[0, 1)$. But in this way, the probability of choosing a point becomes $\frac{1}{2\pi}*1=\frac{1}{2\pi}$ , which is different from $\frac{1}{\pi}$ that I claimed before. Also, in this setup, the expected distance from any point to the center becomes $\frac{1}{2}$, since it is $[0, 1)$ uniform distribution.
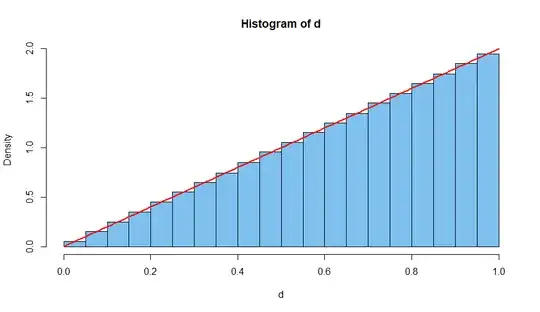
This contradiction gives me trouble and I can only conclude that the distance probability isn't uniform $[0, 1)$ distributed. Actually, from this link http://mathworld.wolfram.com/DiskPointPicking.html
it actually says that "The probability function for distance d from the center of a point picked at random in a unit disk is $P(d) = 2d$.
Indeed, if this is the probability function for distance, the expectation is easy to calculate, $\int_0^1 2rdr=\frac{2}{3}$, which is the same as before. Also, the total probability becomes $\int_0^{2\pi} \int_0^1 2r(\frac{1}{2\pi})rdrd\theta = 1$.
I know why $dxdy = rdrd\theta$ when transforming $x,y$ to $r, \theta$, but it is not that easy to imagine the distance is not uniformly distributed. Can someone give an easy to understand explanation?
Follow-up question, what if the shape of object is more complicated? As an example, if on x-y plane, I draw a equilateral triangle and be asked to uniformly pick a point inside the triangle, how to do it? Previously, I was thinking use rotation matrix. Give the vector representation of two sides, each decides an angle (uniformly between $[0,\frac{\pi}{3}]]$ to rotate. But now I'm very worried that this way, it cannot generate really uniformed distributed points. What if the triangle is not symmetric?
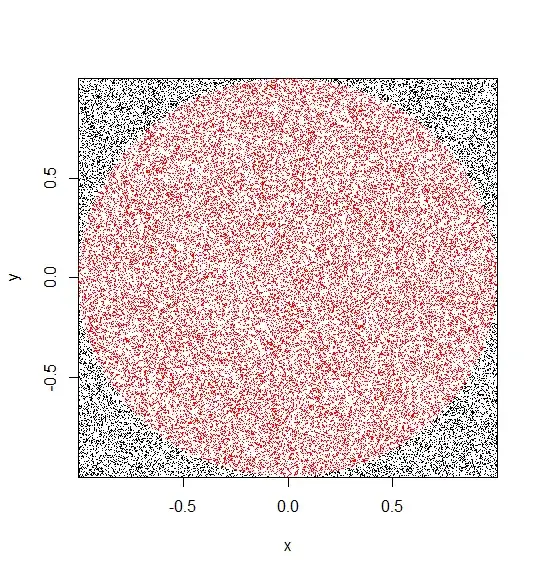
Follow-up question, if this uniform angle and distance cannot generate the desired uniform distributed points in the circle, what if the shape of object is more complicated?
As an example, if on x-y plane, I draw a equilateral triangle and ask to uniformly pick a point inside the triangle, how to do it? Previously, I was thinking use rotation matrix. Give the vector representation of two sides, each decides an angle (uniformly between $[0, \frac{pi}{3}]$ to rotate. Does this still generate uniform distributed points?
– nickdon2006 Sep 10 '17 at 03:37