3

Let $\{e_1,e_2\} $ be standard orthonormal basis of $\Bbb R^2$. Then a new basis $\{E_1,E_2\}$ obtained by $\frac{\pi}{4}$-rotation (counterclockwise) of $\{e_1,e_2\} $ is:

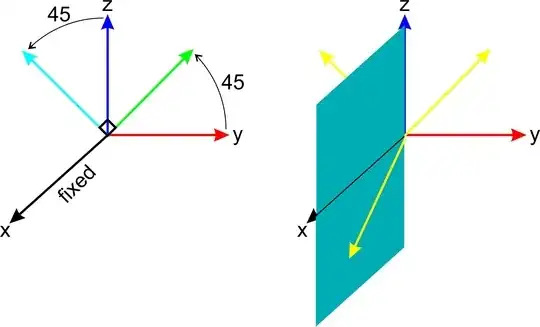
$$R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix}\Rightarrow (E_1,E_2)= \frac{\sqrt{2}}{2}\begin{bmatrix} 1 & 1 \\ -1 & 1 \\ \end{bmatrix}.$$ For example in dim $=3$ the rotation of standard basis are: first rotation in $xy$-plan about $z$-axis and second rotation in direction of old $xz$-plan (before rotation)

enter image description here

I want to know

Question: How to find matrix of $\frac{\pi}{4}$-rotation ($\frac{\pi}{4}$ about every coordinate axis) for $\Bbb R^n$? Does this matrix belongs to ${\rm SO}(n)$ or ${\rm O}(n)$?

C.F.G
  • 8,789
  • 3
    In $\Bbb R^n$, a rotation is not about an axis, it's in a plane. In $\Bbb R^3$, that's the same thing, but in $\Bbb R^4$, rotations aren't about an axis, they're about a plane (unless you want to call that plane the "axis plane", which seems a little strange to me). – Arthur Sep 08 '17 at 11:59
  • What do you mean for a rotation about every coordinate axis. That doesn't seem possible (if you mean a rotation all at once). – Michael Burr Sep 08 '17 at 12:00
  • for example in dim $=3$ the rotation of standard basis are: first rotation in $xy$-plan about $z$-axis and second rotation in direction of old $xz$-plan (before rotation) – C.F.G Sep 08 '17 at 12:06
  • See https://en.wikipedia.org/wiki/Plane_of_rotation – Widawensen Sep 08 '17 at 13:04
  • 1
    The discussion here may be of help to you. – Epiousios Sep 16 '17 at 21:05

1 Answers1

0

Any rotation in $\mathbb{R}^n$ can be represented by a matrix with unit determinant. Also, you can combine any number of rotations by multiplying the matrices they are represented by.

Rotations in $n$ dimensions are represented by a matrix of order $n$, of course.

You could think of it this way: in $\mathbb{R}^3$ you can construct a matrix to rotate any vector along the xy-plane just by placing that matrix you used for $\mathbb{R}^2$ and adding a $[0, 0]^T$ vector to the right, and a $[0, 0, 1]$ to the bottom. You can think of every $n$-th coloumn/row pair as referring to each possible axis.

Carefully placing $\sin$ and $\cos$ in a matrix as you've shown, and leaving 1's on the diagonal, gives you a rotation along a certain plane in $n$ dimensions. And you get the idea that multiplying each matrix will get you the rotation you're looking for.

I'd have inserted more code in this answer, but I'm not that familiar with MathJax.

Niki Di Giano
  • 1,748