$$\ln x - \frac{x}{10} = 0$$
Graph of the equation is as follows:
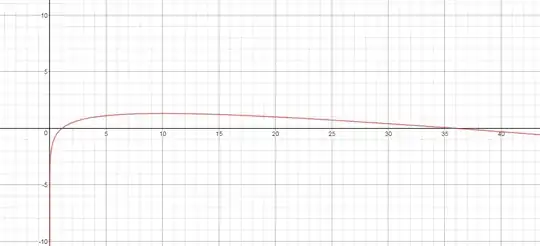
what does $x$ equal to?
Asked
Active
Viewed 368 times
-4
-
1http://www.wolframalpha.com/input/?i=ln(x)+%3D+x+%2F+10 – Sep 06 '17 at 16:05
-
4you can use a numerical method to solve this – Dr. Sonnhard Graubner Sep 06 '17 at 16:09
-
2You can find an approximate solution for the smallest root: take $x = 1 + \epsilon$ then if $\epsilon$ is small we have $\ln(x) \approx \epsilon$ which leads to $\epsilon = 1/9$ and $x = 10/9 = 1.11\cdots$. This turns out to be good to $0.02%$. – Winther Sep 06 '17 at 16:12
-
1Possible duplicate of Approximation to the Lambert W function – Simply Beautiful Art Sep 06 '17 at 16:19
-
We have $x=(\sqrt[10]{e})^x$. If you don't like to use the Lambert W-function you can use the recursion $x_{n+1}=(\sqrt[10]{e})^{x_n}$ with e.g. $x_0:=1$ to get the first solution. For the second solution you can use $x_{n+1}=10\cdot\ln x_n$ with e.g. $x_0:=3$ . – user90369 Sep 06 '17 at 16:30
1 Answers
2
There is not usually any simple solution to this type of equation. One can express the solution in terms of the Lambert $W$ function, but that is not really any help.
Numerical methods can easily produce an approximate answer to any degree of precision. The larger root is very close to 35.77152063957296 and the smaller root is very close to 1.11832559158962974166.
(I did this with no sophisticated techniques at all; I used the “bisection method”, which goes like this: Say that $f(x) = \ln x-\frac x{10}$. We know from your graph that $f(2)> 0$ and $f(100)<0$, and the root is in between. Check the sign of $f(50)$. This is negative, so there must be a root between $2$ and $50$. Now check $f(25)$. This is positive, so the root must be between $25$ and $50$. Repeat as desired.)
MJD
- 67,568
- 43
- 308
- 617
-
1how is the W function not an answer? it IS the answer. many packages evaluate the function and it can be done just by iterating Newtons method – crow Sep 06 '17 at 16:18
-
3@crow It's not an elementary function and most people don't learn about it before taking complex analysis (and perhaps not even then). It's not a (good / useful ) answer at the level this question is asked. – Winther Sep 06 '17 at 16:19
-
4@crow The issue is like saying the solution to $\sin(x)=0,|x|\le\pi/2$ is $x=\arcsin(0)$. To what use is this other than to call it a name when there may exist better solutions? – Simply Beautiful Art Sep 06 '17 at 16:20
-
1The answer on this post has an excellent explanation on this sort of topic. – WaveX Sep 06 '17 at 16:24
-
3Another example is solving $x^2=2^x$ for $x$ in terms of the Lambert W function for $x>0$. Clearly it can be done, but what use is it if we know the solutions are $x=2,4$? – Simply Beautiful Art Sep 06 '17 at 16:24