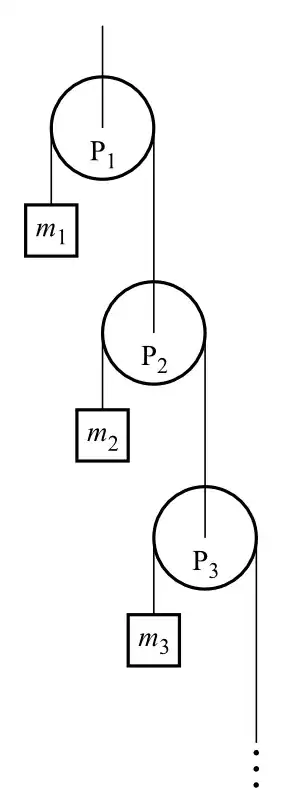
Find the acceleration of any mass for this type of system. At the lowest pulley there are two masses connected, $m_n$ and $m_{n'}$. I having a hard time tackling the finite problem but the solution as $n->\infty$ should be easier. For $m$ is a constant. Need to solve for $T_1$
$$a(P_1) = 0$$ $$T_r = 2T_{r+1}$$ $$a(P_r) = 2\cdot{a(P_{r-1})} - a(m_{r-1})$$ $$a(m_n) = a(P_n)$$
$$a(m_{r}) = g - \frac{T_r}{m} = g - \frac{T_1}{m\cdot{2^{r-1}}}$$
For $n->\infty$,
$$a(m_n) = g$$
So substituting recursively into equation number 3, using the help of equation 1, 4, 6:
$$g + 2^{n-2}\cdot{a(m_{1})} + 2^{n-3}\cdot{a(m_{2})} + ... 2^{0}\cdot{a(m_{n-1})} = 0$$
Please confirm the steps above