1

This may be an elementary question, but I would like to get some clarity on this topic.

My question is about graph structure and its relation to the eigenvalues of the adjacency matrix of the graph.

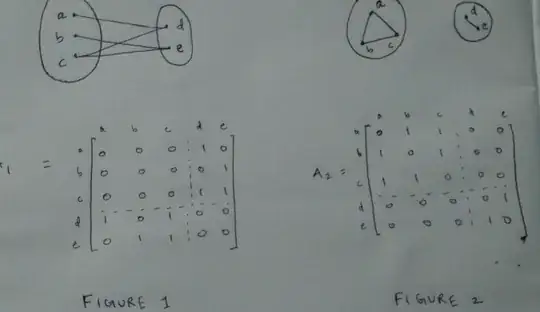
It is well known that for a bipartite graph, the adjacency matrix has a particular block structure (after properly reordering the vertices). A example is shown in figure $1$. Using this block structure, it can be shown that the spectrum of the graph is symmetric about the origin.

Graph structure and adjacency matrix

Another structure is when the graph has clusters. I did a similar example (figure $2$) and in this case also the adjacency matrix has block structure, except that the non zero blocks are along the main diagonal this time. Is there anything interesting that can be said about the spectrum here (like symmetry in the previous case)? Or are these basically the same (can I obtain $A_{1}$ from $A_{2}$ using some permutation? I am guessing no..)

Rodrigo de Azevedo
  • 23,223
TinTin
  • 41
  • Maybe this is of interest to you: https://math.stackexchange.com/questions/21454/prove-that-the-eigenvalues-of-a-block-matrix-are-the-combined-eigenvalues-of-its – Pieter21 Aug 26 '17 at 07:03
  • Thanks..so the eigenvalues of the cluster blocks automatically determine the eigenvalues of the original graph – TinTin Aug 26 '17 at 09:40
  • Can anything more be said here? I was wondering because both $A_{1}$ and $A_{2}$ have a block structure and for $A_{1}$ there is a nice symmetry property.. – TinTin Aug 26 '17 at 09:45

0 Answers0