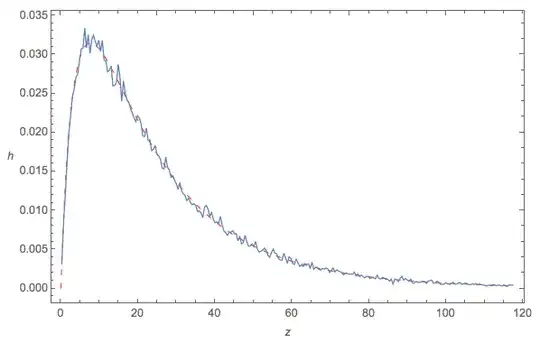
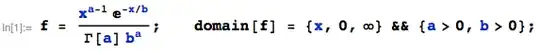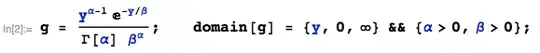In order to provide an analytical derivation and confirm the result, it is possible to proceed as follows:
Let's start by defining independent gamma product $Z_{2}=XY$, $X=Z_{1}$ and $Y=\frac{Z_{2}}{Z_{1}}$. Then we can write joint density using jacobian,
\begin{equation}
f(z_{1},z_{2})=f_{x}(z_{1})f_{y}(z_{2})|J|
\end{equation}
where jacobian $|J|$ is,
\begin{bmatrix}\frac{\partial x }{\partial z_{1}}&\frac{\partial x }{\partial z_{2}}\\\frac{\partial y }{\partial z_{1}}&\frac{\partial y }{\partial z_{2}}\end{bmatrix}
\begin{bmatrix}1&0\\\frac{-z_{2}}{z_{1}^{2}}&\frac{1}{z_{1}}\end{bmatrix}
Then this equals,
\begin{equation}
f(z_{1},z_{2})=f_{x}(z_{1})f_{y}(z_{2})\frac{1}{z_{1}}
\end{equation}
\begin{equation}
f(z_{1},z_{2})=\frac{\beta_{x}^{-\alpha_{x}}z_{1}^{\alpha_{x}-1}e^{\frac{-z_{1}}{\beta_{x}}}}{\Gamma(\beta_{x})}\frac{\beta_{y}^{-\alpha_{y}}(\frac{z_{2}}{z_{1}})^{\alpha_{y}-1}e^{\frac{-z_{2}/z_{1}}{\beta_{y}}}}{\Gamma(\beta_{y})}
\end{equation}
In order to get marginal density of $Z_{2}=XY$ the product, we integrate out the joint density we wrote over $Z_{1}$
\begin{equation}
f(z_{2})=\beta_{x}^{-\alpha_{x}}\beta_{y}^{-\alpha_{y}}z_{2}^{\alpha_{y}-1}\int_{0}^{\infty}\left[\frac{z_{1}^{\alpha_{x}-\alpha_{y}-1}e^{\frac{-z_{1}}{\beta_{x}}}e^{\frac{-z_{2}/z_{1}}{\beta_{y}}}}{\Gamma(\beta_{x})\Gamma(\beta_{y})}dz_{1}\right]
\end{equation}
Using the fact that,
\begin{equation}
\int_{0}^{\infty}x^{\alpha-1}\exp(-ax-bx^{-1})dx=2\left(\frac{b}{a}\right)^{\alpha/2}K_{\alpha}\left(2\sqrt{ab} \right)
\end{equation}
We will have,
\begin{equation}
f\left(z_{2}=xy\right)=\frac{z_{2}^{\alpha_{y}-1}\beta_{x}^{-\alpha_{x}}\beta_{y}^{-\alpha_{y}}2\left(\frac{z_{2}\beta_{x}}{\beta_{y}}\right)^{\frac{\left(\alpha_{x}-\alpha_{y}\right)}{2}}K_{\alpha_{x}-\alpha_{y}}\left(2\sqrt{\frac{z_{2}}{\beta_{x}\beta_{y}}} \right)}{\Gamma(\alpha_{x})\Gamma(\alpha_{y})}
\end{equation}
Another Monte-Carlo check confirms @wolfies nice result above,
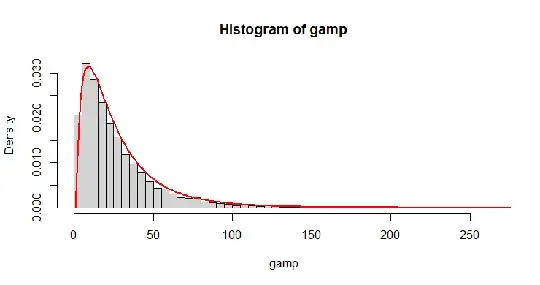
Plus an integral on the pdf confirms the accuracy of it to be the correct density. After integrating in R we obtain,
integrate(gamprod,lower = 0.,upper = Inf,ax = 2,bx = 3,ay = 4,by = 1.1)
1 with absolute error < 6.8e-05