4

After much research and head-scratching to no avail, I was hoping someone here could shed some light on certain properties of the split-complex numbers, namely:

1) Is there any meaningful analog of the triangle inequality for the split-complex numbers using their appropriate definition of modulus?

2) If not, what would be a suitable means by which to check whether (or not) an infinite series of split-complex numbers has a bounded modulus?

The issue I'm having is with the fact that the quadradic form which defines the modulus on the split-complex numbers is not positive-definite. Is it the case that every algebra with a positive-indefinite modulus has no meaningful analog of the triangle inequality?

Any insight into how one might approach this would be greatly appreciated. Reccomendations for reading material would also be more than welcome.

Thanks!

Anixx
  • 10,161
WhiteboardFunk
  • 87

1 Answers1

2

In case of split-complex numbers it is easier to get the reverse triangle inequality than the usual one!

Let us restrict our attention to split-complex numbers $z = a+bj$ with $a^2 \ge b^2$. For them we can define the modulus to be $|z| = \sqrt{a^2-b^2} \in \mathbb{R}^+$. The set of such split-complex numbers form the following blue region on the split-complex plane:

                                                

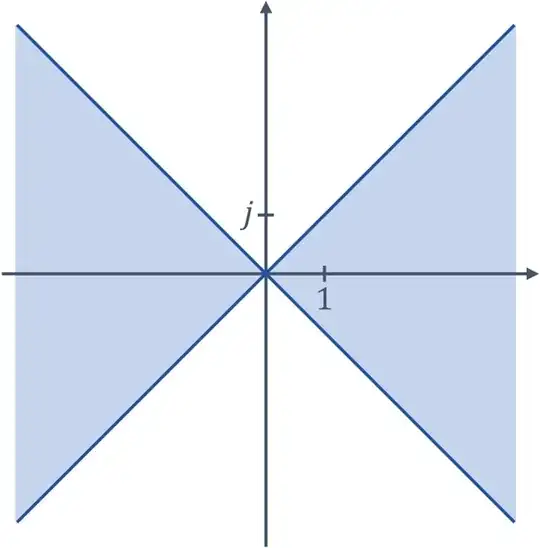
Note that this region is non-convex. So even if both $z_1$ and $z_2$ belong to the blue region, their sum may fall out of this region, and then the modulus $|z_1+z_2|$ will be ill-defined. To fix this issue, we further restrict our attention to one of its convex subregions: either with $a \le 0$ or $a \ge 0$.

           

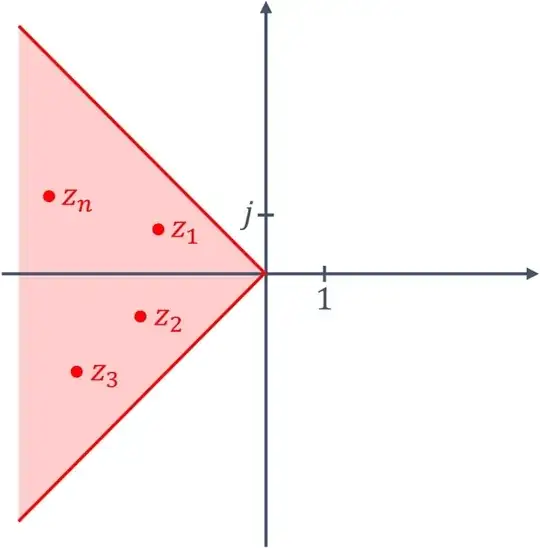
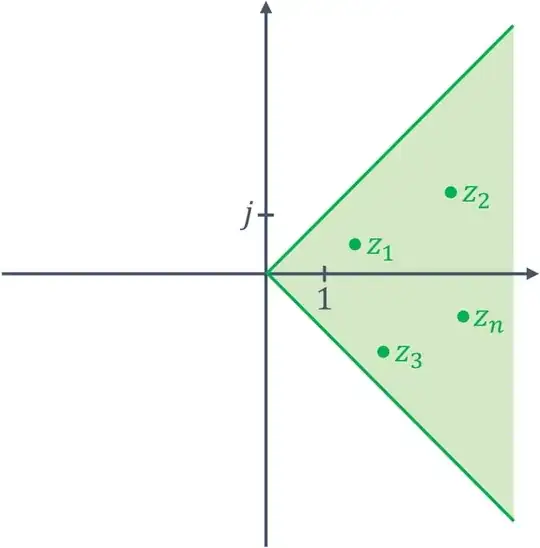
Working within one of these subregions (red or green), one can see that for any $z_1 = a_1 + b_1 j$ and $z_2 = a_2 + b_2 j$ the following inequalities hold:

$$ a_1 a_2 \ge b_1 b_2, \quad \quad (a_1+a_2)^2 \ge (b_1+b_2)^2. \tag{*} $$

Now we start with the obviously true inequality and go step by step:

$$ 0 \le (a_1b_2 - a_2 b_1)^2, $$ $$ -(a_1b_2)^2-(a_2b_1)^2 \le -2a_1a_2b_1b_2, $$ $$ \color{gray}{ (a_1a_2)^2+(b_1b_2)^2}-(a_1b_2)^2-(a_2b_1)^2 \le \color{gray}{ (a_1a_2)^2+(b_1b_2)^2}-2a_1a_2b_1b_2, $$ $$ (a_1^2-b_1^2)(a_2^2-b_2^2) \le (a_1a_2-b_1b_2)^2 $$ $$ \Downarrow \text{ using (*)} $$ $$ \sqrt{(a_1^2-b_1^2)(a_2^2-b_2^2)} \le (a_1a_2-b_1b_2), $$ $$ 2\sqrt{(a_1^2-b_1^2)(a_2^2-b_2^2)} \le 2 a_1a_2-2b_1b_2, $$ $$ \color{gray}{a_1^2-b_1^2+a_2^2-b_2^2}+ 2\sqrt{(a_1^2-b_1^2)(a_2^2-b_2^2)} \le \color{gray}{a_1^2-b_1^2+a_2^2-b_2^2} + 2 a_1a_2-2b_1b_2, $$ $$ \left(\sqrt{a_1^2-b_1^2}+\sqrt{a_2^2-b_2^2}\right)^2 \le (a_1+a_2)^2-(b_1+b_2)^2 $$ $$ \Downarrow \text{ using (*)} $$ $$ \sqrt{a_1^2-b_1^2}+\sqrt{a_2^2-b_2^2} \le \sqrt{(a_1+a_2)^2-(b_1+b_2)^2}. $$ So we get the reverse triangle inequality: $$ |z_1|+|z_2| \le |z_1+z_2|. $$

It is easy to show by induction that if all $\{z_n\}$ belong to the same convex region (red or green), then the reverse triangle inequality still holds:

$$ \sum|z_n| \le \left| \sum z_n \right|. $$

In contrast to that, the usual triangle inequality $|z_1| + |z_2| > |z_1 + z_2|$ may hold only if $z_1$ and $z_2$ belong to different regions (e.g., $z_1 \in$ red, $z_2 \in$ green). Note that such an arrangement cannot be continued by induction, so it seems that no simple conditions for $\sum|z_n| > \left| \sum z_n \right|$ can be found. I believe that (in case of split-complex numbers with $|z| \in \mathbb{R}^+$) it is more natural to work with the reverse triangle inequality than with the usual one.

Zeekless
  • 1,599
  • 10
  • 18