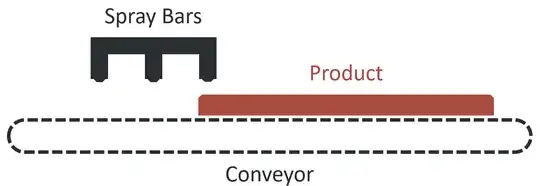
A product is initially at rest on a conveyor belt:
The initial conditions of the product can be described as follows:$$x_i=0$$ $$v_i=0$$ $$a_i=0$$$$j_i = j⋆ $$.
The product will be moved forward distance of exactly Δx (known) to position it under the conveyor belt:
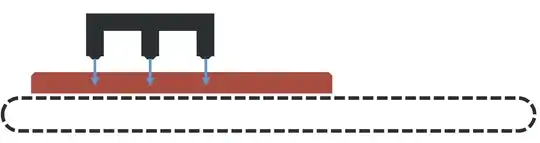
When the movement is complete, the product will be sprayed for a few moments, so it must come to a complete rest at this point:
The conveyor, which must move the product into position, will complete the movement in the minimum time possible.
The conveyor's control system will apply a constant jerk of j⋆ (known), -j⋆ (known) or zero.
However, the conveyor must obey these limits:
- It has a max velocity of
v⋆(known), - a max acceleration of
a⋆(known), - a max deceleration of
d⋆(known).
Assume the product does not slide or slip on the conveyor.
How long will it take the product to complete the movement of Δx?
Side Note:
At first glance, it seems as though the problem can be solved by a simple application of the kinematic equation for one-dimensional motion with constant jerk (and its derivatives):
$$x = x_0 + v_0 t + \frac{1}{2} a_0 t^2 + \frac{1}{6}jt^3$$
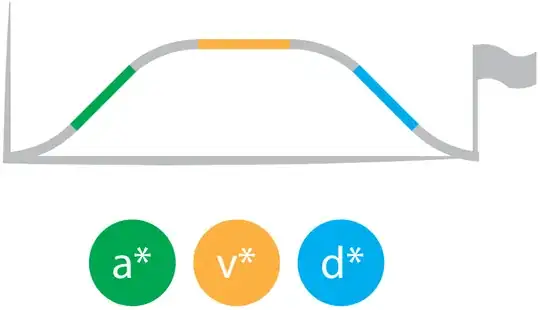
However, the limits v⋆, a⋆ and d⋆ pose a major problem. For some values of Δx, the conveyor may not even reach max velocity, max acceleration, or max deceleration. Therefore, there will be 8 possible scenarios in which different combinations of these limits are reached. To assist with this part of the problem, I have created a decision chart that illustrates the different possible scenarios:
As Δx gets smaller and smaller, the possibilities range from all three limits reached...
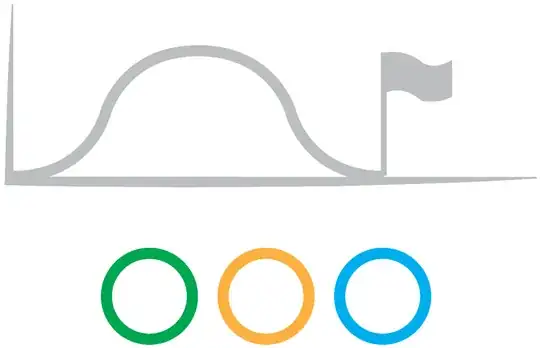
... to no limits reached...
... making it hard to describe the time passed during the movement with a single function. I am stumped at this point- how do I predict which limits will be met and which will not?

x'''will look like in order for the movement to take the minimum amount of time. – Luminaire Jul 24 '17 at 18:57