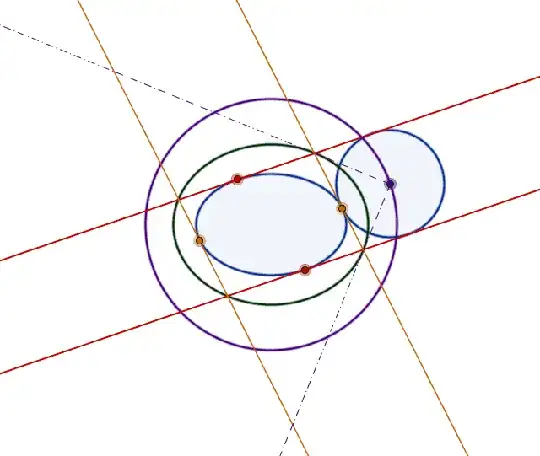
A friend of mine showed me the following problem:
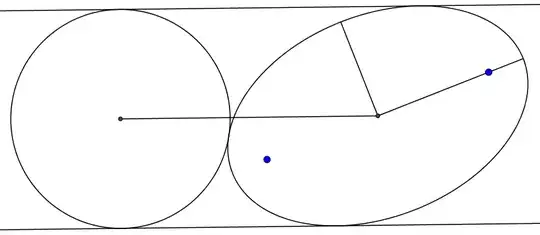
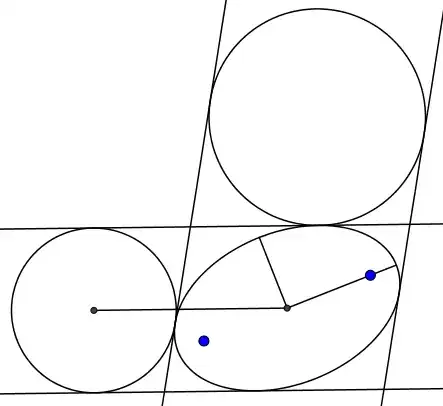
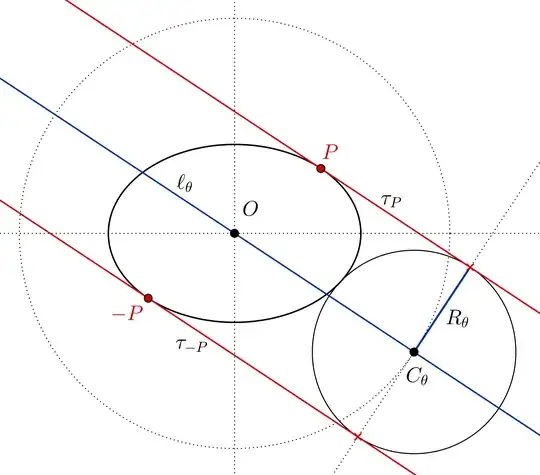
Let $\cal E$ be an ellipse whose semi major axis has length $a$ and semi minor axis has length $b$. Let $\ell_1, \ell_2$ be two parallel lines tangent to $\cal E$. Let $\cal C$ be the circle tangent to $\ell_1$, $\ell_2$, and $\cal E$. Prove that the distance between the centers of $\cal C$ and $\cal E$ is equal to $a+b$.
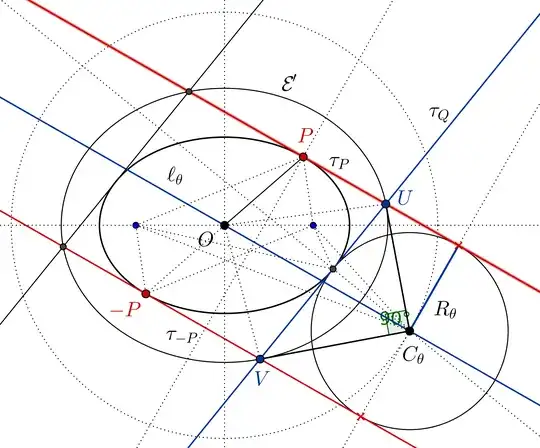
So far I managed to prove that if we draw the tangent line $k_1$ through $\cal E \cap \cal C$ and the tangent $k_2$ to $\cal E$ parallel to $k_1$ then the circle tangent to $k_1, k_2, \ell_1$ is tangent to $\cal E$ as well.
I'm stuck. I'd like to see some proofs, preferably non-analytic ones.