Question: Let $A(n)$ be a finite square $n \times n$ matrix with entries $a_{ij}=1$ if $i+j$ is a perfect power; otherwise equals to $0$. Is it true that $${1 \above 1.5 pt n^2}\sum_{i=1}^n \sum_{j=1}^n a_{ij} \leq {1 \above 1.5pt 3}$$ with equality holding if and only if $n=3$ or $n=6$ ?
Let $A(n)$ be a finite square $n \times n$ matrix with entries $a_{ij}=1$ if $i+j$ is a perfect power; otherwise equals to $0$. For an example consider $A(5)$
$$A(5)= \text{ }\begin{pmatrix} 0&0&1&0&0\\ 0&1&0&0&0\\ 1&0&0&0&1\\ 0&0&0&1&1\\ 0&0&1&1&0\\ \end{pmatrix}$$
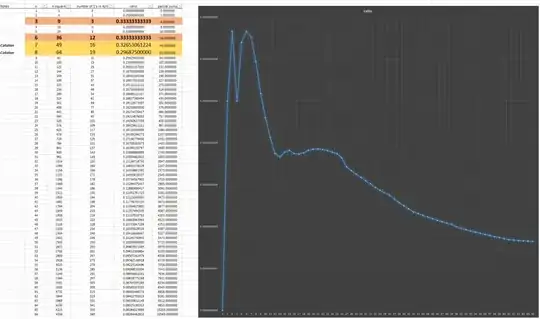
Can we show that ${1 \above 1.5 pt n^2}\sum_{i=1}^n \sum_{j=1}^n a_{ij} \leq {1 \above 1.5pt 3}$ with equality holding if and only if $n=3$ or $n=6$. The graph below plots the values of ${1 \above 1.5 pt n^2}\sum_{i=1}^n \sum_{j=1}^n a_{ij}$ for small $n$. The graph is what motivated me to ask the question. It appears that the maximums are achieved if $n=3$ or $n=6$.
UPDATE: I have corrected several terms and added several new terms check out: A293462.
Here was my approach: Let $^t$ be the transpose map that sends the entry $a_{ij} \to a_{ji}$. The commutativity of addition shows us that if $i+j$ is a perfect power then so is $j+i$. Equivalently we see that $a_{ij}=a_{ji}$. In particular $A(n)^t=A(n)$ and so $A(n)$ is symmetric. Now observe that $(a_{ij})^2=a_{ij}$. Since $A(n)$ is symmetric $A(n)^tA(n)=A(n)^2$. The following result is easy to show $$\sum_{i=1}^n \sum_{j=1}^n a_{ij}=tr(A(n)^2)$$ Similarly it easy to show that if ${1 \above 1.5 pt n^2}\sum_{i=1}^n \sum_{j=1}^n a_{ij}={1 \above 1.5 pt x}$ then $x$ is a divisor of $n$. Assume ${tr(A(n)^2) \above 1.5pt n^2}={1 \above 1.5pt 3}$ then $3$ divides $n$. We start by showing via inspection the base case of $n=3$ and $n=6$. Suppose $n=3$ then
$$A(3)^2= \text{ } \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{pmatrix}$$
And so $tr(A(3)^2)=3$. Surely ${3 \above 1.5pt 3^2}={1 \above 1.5 pt 3}$. Similarly it is easy to compute and show that if $n=6$
$$A(6)^2= \text{ }\begin{pmatrix} 1&0&0&0&1&1\\ 0&2&1&0&0&1\\ 0&1&3&1&0&0\\ 0&0&1&2&1&0\\ 1&0&0&1&2&1\\ 1&1&0&0&1&2\\ \end{pmatrix} $$
And from this we can see that $tr(A(6)^2)=12$. And again we have that ${12 \above 1.5pt 6^2}={1 \above 1.5 pt 3}$.
Assume $n\neq 3$ and $n\neq 6$. Now since ${tr(A(n)^2) \above 1.5pt n^2}={1 \above 1.5pt 3}$ we know that $3\times tr(A(n)^2)=n^2$. If $a_{ii}$ is any entry on the diagonal of $A(n)^2$ then explictly $3(a_{11}+ \ldots +a_{nn})=n^2$ so $\sqrt{3}\sqrt{a_{11}+\ldots + a_{nn}}=n$ and consequently $\sqrt{3} \mid \sqrt{a_{11}+\ldots + a_{nn}}$ otherwise $n$ is not an integer which is a contradiction.
^Update 1: The argument scratched out above is wrong thanks to commentator @SEWillB. ^Update 2: The argument previously scratched out above is correct. See edits.
That is all I can come up with - and it might not be the best approach and possibly the problem is trivial and I am just missing it. It could also be wrong. The picture below provides some data for small values of $n$.