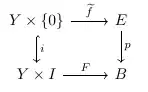Smooth fibration is a submersion

Question

in Wikipedia and the following questions: [1], [2] or their respective answers or comments it is said that a smooth fibration is a submersion. To make clear what I mean:

Definition. A smooth map $p\colon E \to B$ is said to satisfy the homotopy lifting property in the smooth category if given the following commutative diagram where all maps are smooth:

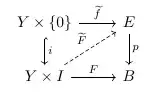
there exists an smooth map $\widetilde{F}$ making the following diagram smooth:

Definition. A smooth map is said to be a smooth (Hurewicz) fibration if it satisfies the homotopy lifting property in the smooth category for all manifolds $Y$.

Definition. A smooth map is said to be a smooth Serre fibration if it satisfies the homotopy lifting property in the smooth category for all discs $I^n$, $n\ge 0$.

Question. Could you please help me to understand why smooth Serre fibrations or smooth Hurewicz fibrations are submersions.

I have tried using the characteristic property of submersions and so on.....but I haven't been able to prove anything.

By the way, I know that the projections in smooth fiber bundles are smooth submersions. That is straightforward. But I would like to generalize it to fibrations.

Remark. If necessary we can assume both $B$ and $E$ are compact since it is the case I am interested in.

Answer 1

Let $x$ be a point of $B$, consider a chart $f:U\simeq I^n\rightarrow B$ whose domain contains $x$ and $f(0)=x$. Write $Y=\{x\}$ and consider a point $z\in p^{-1}(x)$. You can define $\tilde f:Y\times \{0\}\rightarrow E$ by $\tilde f(x,0)=z$. Let $F:\{x\}\times I^n\rightarrow B$ defined by $F(x,y)=f(x)$. We have $p\circ \tilde f=F\circ i$. The homotopy lifting property implies the existence of $H:\{x\}\times U\rightarrow E$ such that $p\circ H=f$. Since the tangent map $df_0:T_0\mathbb{R}^n\rightarrow T_xB$ is bijective, and $df_0=dp_z\circ dH_{(0,x)}$, we deduce that $dp_z$ is surjective, and henceforth $p$ is a submersion.