Smoothstep sigmoid-like function: Can anyone prove this relation?

Question

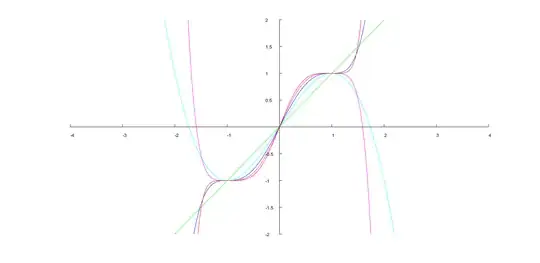
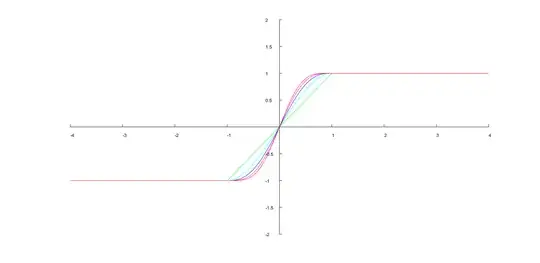
The Smoothstep sigmoid-like function is defined as the polynomial

$$ \begin{align} \operatorname{S}_N(x) &= x^{N+1} \sum_{n=0}^{N} \binom{N+n}{n} \binom{2N+1}{N-n} (-x)^{n} \qquad N \in \mathbb{Z} \ge 0 \\ &= \sum_{n=0}^{N} (-1)^n \binom{N+n}{n} \binom{2N+1}{N-n} x^{N+n+1} \\ &= \sum_{n=0}^{N} \binom{-N-1}{n} \binom{2N+1}{N-n} x^{N+n+1} \\ \end{align} $$

The first 7 examples are:

$$\begin{align} \operatorname{S}_0(x) &= x \\ \operatorname{S}_1(x) &= -2x^3 + 3x^2 \\ \operatorname{S}_2(x) &= 6x^5 - 15x^4 + 10x^3 \\ \operatorname{S}_3(x) &= -20x^7 + 70x^6 - 84x^5 + 35x^4 \\ \operatorname{S}_4(x) &= 70x^9 - 315x^8 + 540x^7 - 420x^6 + 126x^5 \\ \operatorname{S}_5(x) &= -252x^{11} + 1386x^{10} - 3080x^9 + 3465x^8 - 1980x^7 + 462x^6 \\ \operatorname{S}_6(x) &= 924x^{13} - 6006x^{12} + 16380x^{11} - 24024x^{10} + 20020x^9 - 9009x^8 + 1716x^7 \\ \\ \end{align} $$

It is purported, for all non-negative integer $N$, that $\operatorname{S}_N(0) = 0$ and $\operatorname{S}_N(1) = 1$ and, at those two points, as many derivatives equal zero as possible. I think it is also purported that $\operatorname{S}_N(\tfrac12) = \tfrac12$ and that this polynomial display odd-symmetry about the point at $x=\tfrac12$

If we define a linearly-scaled and offset version of the Smoothstep polynomial as:

$$ \operatorname{R}_N(x) = 2\operatorname{S}_N\left( \tfrac12(x+1) \right) - 1 $$

Then this means that $\operatorname{R}_N(-1) = -1$, $\operatorname{R}_N(1) = 1$, and as many derivatives as possible at those two points are zero. And we see that $\operatorname{R}_N(0) = 0$ and that odd-symmetry exists: $\operatorname{R}_N(-x) = -\operatorname{R}_N(x)$

Can anyone show, with the least amount of pain possible, that the derivative of $\operatorname{R}_N(x)$ becomes

$$\begin{align} \operatorname{R}^{'}_{N}(x) &= \operatorname{S}^{'}_{N}\left( \tfrac12(x+1) \right) \\ &= \left( \sum\limits_{n=0}^{N} \frac{N!}{n! (N-n)!} \frac{(-1)^n}{2n+1} \right)^{-1} (1-x^2)^{N} \qquad ? \\ \end{align}$$

This is not homework (I haven't been in skool since the early '80s). This DSP question and answer show the previous work I have done with this. It's just a little bit bitchy and I am not sure the least painful way to go about doing this.

I guess that I am trying to show that

$$\begin{align} \operatorname{S}^{'}_{N}\left( \tfrac12(x+1) \right) &= \sum_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n}(N+n+1) \left(\tfrac12(x+1)\right)^{N+n} \\ &= \left( \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \frac{(-1)^n}{2n+1} \right)^{-1} (1-x^2)^{N} \\ \end{align}$$

This really looks like a copulating female canine to me.

---

EDIT:

Here is the clearest way for me to state the question:

Let $x \in \mathbb{R}, \ N \ge 0 \in \mathbb{Z}$.

Define:

$$\begin{align} f_N & \triangleq \int\limits_{0}^{1} \big(1 - u^2 \big)^{N} \ du \\ & = \sum\limits_{n=0}^{N} \binom{N}{n} \frac{(-1)^n}{2n+1} \\ \end{align}$$

Define:

$$ \operatorname{R}_N(x) \triangleq \frac{1}{f_N} \int\limits_{0}^{x} \big(1 - u^2 \big)^{N} \ du $$

Define from the Wikipedia definition of the Smoothstep sigmoid-like function:

$$\operatorname{S}_N(x) \triangleq \sum\limits_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n} x^{N+n+1} $$

Prove:

$$ \operatorname{R}_N(x) = 2\operatorname{S}_N\big(\tfrac12 (x+1) \big) - 1 $$

It suffices to prove that their first derivatives of the left-hand and right-hand sides are equal, because we know the left-hand and right-hand sides are equal at $x=-1$. This means it is sufficient to show that:

$$ \frac{1}{f_N} (1-x^2)^{N} = \frac{d}{du}\,\operatorname{S}_N(u) \Bigg|_{u=\frac12 (x+1)} $$

or

$$ \frac{1}{f_N} (1-x^2)^{N} = \sum_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n} (N+n+1) \left(\tfrac12(x+1)\right)^{N+n} $$

or, explicitly:

$$ \left( \sum\limits_{n=0}^{N} \binom{N}{n} \frac{(-1)^n}{2n+1} \right)^{-1} (1-x^2)^{N} = \sum_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n} (N+n+1) \left(\tfrac12(x+1)\right)^{N+n} $$

Answer 1

We want to show for $N\geq 0$

\begin{align*} \color{blue}{\left(\sum_{n=0}^N\right.}&\color{blue}{\left.\binom{N}{n}\frac{(-1)^n}{2n+1}\right)^{-1}(1-x^2)^N}\\ &=\color{blue}{\sum_{n=0}^N\binom{-N-1}{n}\binom{2N+1}{N-n}(N+n+1)\left(\frac{1}{2}(x+1)\right)^{N+n}}\tag{1}\\ \end{align*}

We start with the RHS and obtain \begin{align*} \sum_{n=0}^N&\binom{-N-1}{n}\binom{2N+1}{N-n}(N+n+1)\left(\frac{1}{2}(x+1)\right)^{N+n}\\ &=\sum_{n=0}^N(-1)^n\binom{N+n}{n}\binom{2N+1}{N+n+1}(N+n+1)\left(\frac{1}{2}(x+1)\right)^{N+n}\tag{2}\\ &=(2N+1)\sum_{n=0}^N(-1)^n\binom{N+n}{n}\binom{2N}{N+n}\left(\frac{1}{2}(x+1)\right)^{N+n}\tag{3}\\ &=(2N+1)\binom{2N}{N}\sum_{n=0}^N(-1)^n\binom{N}{n}\left(\frac{1}{2}(x+1)\right)^{N+n}\tag{4} \end{align*}

Comment:

• In (2) we use the binomial identity $\binom{-p}{q}=\binom{p+q-1}{q}(-1)^q$.

• In (3) we use the binomial identity $\binom{p}{q}=\frac{p}{q}\binom{p-1}{q-1}$.

• In (4) we use the binomial identity $\binom{p}{m}\binom{m}{q}=\binom{p}{q}\binom{p-q}{m-q}$

With (4) the claim (1) boils down to show

\begin{align*} \color{blue}{\left(\sum_{n=0}^N\right.}&\color{blue}{\left.\binom{N}{n}\frac{(-1)^n}{2n+1}\right)^{-1}(1-x^2)^N}\\ &=\color{blue}{(2N+1)\binom{2N}{N}\sum_{n=0}^N(-1)^n\binom{N}{n}\left(\frac{1}{2}(x+1)\right)^{N+n}}\tag{5}\\ \end{align*}

Intermezzo:

We can find a closed formula for the denominator of the LHS. The following is valid: \begin{align*} \sum_{n=0}^N\binom{N}{n}\frac{(-1)^n}{2n+1}=\frac{4^N}{2N+1}\binom{2N}{N}^{-1}\tag{6} \end{align*}

A proof is given in the appendix.

Using (6) and since $(1-x^2)^N=(1-x)^N(1+x)^N$ the equation (5) can be simplified to

\begin{align*} \color{blue}{\frac{1}{2^N}(1-x)^N =\sum_{n=0}^N\frac{(-1)^n}{2^n}\binom{N}{n}(x+1)^{n}} \end{align*}

Applying the binomial theorem to the RHS we finally get

\begin{align*} \sum_{n=0}^N\frac{(-1)^n}{2^n}\binom{N}{n}(x+1)^{n}&=\sum_{n=0}^N\binom{N}{n}\left(-\frac{1+x}{2}\right)^{n}\\ &=\left(1-\frac{1+x}{2}\right)^N\\ &=\frac{1}{2^N}(1-x)^N \end{align*}

and the claim (1) follows.

We now prove formula (6) following chapter I (problem section, problem 4 with solution) in Combinatorial Identities by John Riordan.

Appendix: The following is valid \begin{align*} \qquad\qquad\sum_{n=0}^N\binom{N}{n}\frac{(-1)^n}{2n+1}=\frac{4^N}{2N+1}\binom{2N}{N}^{-1}\qquad\qquad N\geq 0 \end{align*}

We obtain using the Kronecker delta $\delta_{N,0}$ \begin{align*} f_N=\sum_{n=0}^N(-1)^n\binom{N}{n}\frac{1}{2n+1}&=\sum_{n=0}^N(-1)^n\binom{N}{n}\left(1-\frac{2n}{2n+1}\right)\\ &=\delta_{N,0}-\sum_{n=0}^N(-1)^n\binom{N}{n}\frac{2n}{2n+1}\tag{7}\\ &=\delta_{N,0}-2N\sum_{n=1}^N(-1)^n\binom{N-1}{n-1}\frac{1}{2n+1}\tag{8}\\ \end{align*}

Comment:

• In (7) we apply $\binom{p}{q}=\frac{p}{q}\binom{p-1}{q-1}$.

We also get \begin{align*} f_N=\sum_{n=0}^N(-1)^n\binom{N}{n}\frac{1}{2n+1} &=\sum_{n=0}^N(-1)^n\left[\binom{N-1}{n}+\binom{N-1}{n-1}\right]\frac{1}{2n+1}\\ &=f_{N-1}+\sum_{n=1}^N(-1)^n\binom{N-1}{n-1}\frac{1}{2n+1}\tag{9}\\ \end{align*}

Adding (8) and $2N$ times (9) we get \begin{align*} \qquad\qquad(2N+1)f_N=2Nf_{N-1}+\delta_{N,0}\qquad\qquad N\geq 0\tag{10} \end{align*}

Iterating (10) we obtain with $f_0=1$ for $N>0$ \begin{align*} f_N&=\frac{2N}{2N+1}f_{N-1}=\frac{(2N)(2N-2)}{(2N+1)(2N-1)}f_{N-2}=\ldots\\ &=\frac{(2N)!!}{(2N+1)!!}\\ &=\frac{(2N)!!(2N)!!}{(2N+1)!}\\ &=\frac{1}{2N+1}\cdot\frac{2^{2N}N!N!}{(2N)!}\\ &=\frac{4^N}{2N+1}\binom{2N}{N}^{-1} \end{align*} and the claim (6) follows.

Here we use double factorials \begin{align*} (2N)!!&=(2N)(2N-2)\cdots4\cdot 2\\ (2N+1)!!&=(2N+1)(2N-1)\cdots 3\cdot 1\\ \end{align*} and the formulae \begin{align*} (2N)!&=(2N)!!(2N-1)!!\\ (2N)!!&=2^NN! \end{align*}

Answer 2

Here is shown the development of the odd-symmetric Smoothstep function:

$$\operatorname{R}_N(x) = \begin{cases} -1 & x < -1 \\ \frac{1}{f_N} \int\limits_{0}^{x} \big(1 - u^2 \big)^{N} \ du \quad & -1 \le x \le 1 \\ +1 & 1 < x \\ \end{cases}$$

where $x \in \mathbb{R}, \ N\ge0 \in \mathbb{Z},$ and $\tfrac{1}{f_N}$ is a scaling constant judiciously chosen so that $\operatorname{R}_N(x)$ is continuous and $\operatorname{R}_N(\pm 1) = \pm 1$.

$$ f_N = \int\limits_{0}^{1} \big(1 - u^2 \big)^{N} \ du $$

Since the integrand is positive for $|u| < 1$, this is a monotonic increasing function. It is also clear that odd-symmetry prevails:

$$ \operatorname{R}_N(-x) = -\operatorname{R}_N(x) \qquad \forall x \in \mathbb{R}, \ N\ge0 \in \mathbb{Z} $$

This odd-symmetric Smoothstep function is, I believe, directly related to the commonly-defined Smoothstep sigmoid-like function as

$$ \operatorname{R}_N(x) = 2\operatorname{S}_N\big(\tfrac12 (x+1) \big) -1 \qquad -\infty < x < +\infty $$

where

$$\operatorname{S}_N(x) = \begin{cases} 0 & x < 0 \\ \sum\limits_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n} x^{N+n+1} \quad & 0 \le x \le 1 \\ 1 & 1 < x \\ \end{cases}$$

for $x \in \mathbb{R}, \ N\ge0 \in \mathbb{Z}$ . This relationship is what I want rigorously proven. (Or, at least, a decent amount of rigor.)

For $|x| < 1$ the 1st derivative of $\operatorname{R}_N(x)$ is

$$ \operatorname{R}_N^{'}(x) = \tfrac{1}{f_N} \big(1 - x^2 \big)^{N} $$

The 2nd derivative of $\operatorname{R}_N(x)$ is

$$ \operatorname{R}_N^{''}(x) = \tfrac{1}{f_N} N \big(1 - x^2 \big)^{N-1} (-2x)$$

The 3rd derivative of $\operatorname{R}_N(x)$ is

$$\begin{align} \operatorname{R}_N^{'''}(x) &= \tfrac{1}{f_N} N(N-1) \big(1 - x^2 \big)^{N-2} (-2x)^2 \ + \ \tfrac{1}{f_N} N \big(1 - x^2 \big)^{N-1} (-2) \\ &= \tfrac{1}{f_N} \big(1 - x^2 \big)^{N-2} \bigg( N(N-1)(-2x)^2 - 2N(1 - x^2) \bigg) \\ \end{align}$$

and, for $n \ge 1$, the $n$th derivative is

$$ \operatorname{R}_N^{(n)}(x) = \tfrac{1}{f_N} \big(1 - x^2 \big)^{N-n+1} \, g_n(x) $$

where $g_n(x)$ is some ($n$-1)th order polynomial function of $x$ and is finite in value. This can be proven inductively by considering the ($n$+1)th derivative:

$$\begin{align} \\ \operatorname{R}_N^{(n+1)}(x) &= \tfrac{d}{dx} \Big( \operatorname{R}_N^{(n)}(x) \Big) \\ &= \tfrac{d}{dx} \Big(\tfrac{1}{f_N} \, \big(1 - x^2 \big)^{N-n+1} \, g_n(x)\Big) \\ &= \tfrac{1}{f_N}(N-n+1)\big(1 - x^2 \big)^{N-n} (-2x) g_n(x) \, + \, \tfrac{1}{f_N} \big(1-x^2 \big)^{N-n+1}g'_n(x) \\ &= \tfrac{1}{f_N} \big(1 - x^2 \big)^{N-n} \Big( (N-n+1)(-2x) g_n(x) \, + \, (1-x^2) g'_n(x) \Big) \\ &= \tfrac{1}{f_N} \big(1 - x^2 \big)^{N-n} \, g_{n+1}(x) \\ \\ \end{align}$$

where $ g_{n+1}(x) = (N-n+1)(-2x) g_n(x) + (1-x^2) g'_n(x) $ .

Because of differentiation, the order of polynomial $g'_n(x)$ is one less than the order of $g_n(x)$, but polynomial $(1-x^2)g'_n(x)$ is one order greater than $g_n(x)$ and so also is $(-2x) g_n(x)$.

When $x = \pm 1$, then the first $N$ derivatives are zero, $$ \operatorname{R}^{(n)}(x) \Bigg|_{x=\pm 1} = 0 \qquad \text{for } 1 \le n \le N $$ making this polynomial maximally flat at $x = \pm 1$.

The integrand is a binomial and can be expressed as a power series using binomial expansion:

$$\begin{align} \big(1 - u^2 \big)^{N} & = \sum\limits_{n=0}^{N} \binom{N}{n} \big(-u^2\big)^n (1)^{N-n} \\ & = \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \big(-u^2\big)^n (1)^{N-n} \\ & = \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} (-1)^n u^{2n} \\ \end{align}$$

So the integral can be expressed as an integral of a power series:

$$\begin{align} \int\limits_{0}^{x} \big(1 - u^2 \big)^{N} \ du & = \int\limits_{0}^{x} \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} (-1)^n u^{2n} \ du \\ & = \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} (-1)^n \int\limits_{0}^{x} u^{2n} \ du \\ & = \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \frac{(-1)^n}{2n+1} u^{2n+1} \Bigg|_0^x \\ & = \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \frac{(-1)^n}{2n+1} x^{2n+1} \\ & = x \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \frac{(-1)^n}{2n+1} \big(x^2 \big)^n \\ \end{align}$$

When $x = \pm 1$, we get

$$ \int\limits_{0}^{\pm 1} \big(1 - u^2 \big)^{N} \ du = \pm \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \frac{(-1)^n}{2n+1} $$

This makes the scaler $f_N$ to be

$$\begin{align} f_N &= \sum\limits_{n=0}^{N} \frac{N!}{n!(N-n)!} \frac{(-1)^n}{2n+1} \\ &= \frac{4^N}{2N+1}\binom{2N}{N}^{-1} \\ &= \frac{4^N \ (N!)^2}{(2N+1)!} \\ \end{align}$$

(the closed form is because of the Proof in the Appendix of the accepted answer here) and makes the odd-symmetric Smoothstep function to be:

$$ \operatorname{R}_N(x) = \frac{(2N+1)!}{4^N \ N!} \ \sum\limits_{n=0}^{N} \frac{(-1)^n}{(2n+1)n!(N-n)!} x^{2n+1} $$

for $|x| \le 1$ .

The Smoothstep polynomials (without splicing to the $\operatorname{sgn}(x) = \pm 1$ saturated components) look like

I think the order $2N+1$ starts at 1 and goes to 9 (or $0 \le N \le 4$)

With the saturation attached, the Smoothstep sigmoid-like curves look like

The odd-symmetry Smoothstep function is continuous everywhere and all derivatives, up to the $N$th derivative, are continuous everywhere and the ($N$+1)th derivative and higher are continuous everywhere except where the constant saturation is spliced to the polynomial at $x = \pm 1$.

What I want to be able to prove is that the two definitions of these Smoothstep polynomials are equivalent, given the proper scaling and offset of $x$.

$$\begin{align} \operatorname{R}_N(x) &= 2\operatorname{S}_N\big(\tfrac12(x+1)\big)-1 & -\infty < x < +\infty \\ \\ \frac{(2N+1)!}{4^N \ N!} \sum\limits_{n=0}^{N} \frac{(-1)^n}{(2n+1)n!(N-n)!} x^{2n+1} &= 2 \sum\limits_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n} \big(\tfrac12(x+1)\big)^{N+n+1} - 1 & -1 \le x \le 1 \\ \end{align}$$

Because it is not hard to show equality at $x=-1$, to show both sides as equivalent, it suffices to show their derivatives as equivalent (with the proper scaling and offset of $x$). So it suffices to prove that

$$ \frac{(2N+1)!}{4^N \ (N!)^2} \big( 1-x^2 \big)^{N} = \sum_{n=0}^{N} \binom{-N-1}{n}\binom{2N+1}{N-n} (N+n+1) \left(\tfrac12(x+1)\right)^{N+n} $$

This is what the bounty was for.

Answer 3

I do not know how much this could help you.

What it seems it that, using $$S_n(x)=\sum_{i=0}^{n-1} \binom{-n}{i} \binom{2 n-1}{n-i-1} x^{n+i}=n \binom{2 n-1}{n-1} B_x(n,n)$$ where appears the incomplete beta function. $$S_n\left(\frac{x+1}2\right)=n \binom{2 n-1}{n-1} B_{\frac{x+1}{2}}(n,n)$$ $$R_n(x)=2 n \binom{2 n-1}{n-1} B_{\frac{x+1}{2}}(n,n)-1 $$ $$S^{'}_n\left(\frac{x+1}2\right)=\frac{\Gamma \left(n+\frac{1}{2}\right)}{\sqrt{\pi } \, \Gamma (n)}\left(1-x^2\right)^{n-1} $$ $$R^{'}_n(x)=\frac{2 \Gamma \left(n+\frac{1}{2}\right)}{\sqrt{\pi }\, \Gamma (n)}\left(1-x^2\right)^{n-1}$$
I hope and wish no mistakes on my side.