0

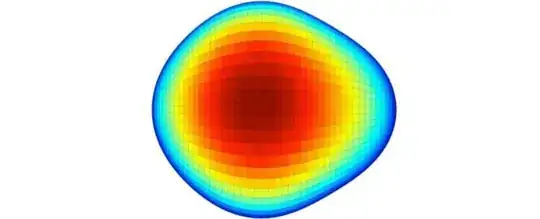
I am thinking how to write the shape of pear-shape atom mass mathematically and/or MATLAB. The picture can be made in MATLAB where x-axis is time, and y-axis can be potential/energy/... The paper Direct Evidence of Octupole Deformation in Neutron-Rich 144B is about a physical finding.

enter image description here

TZakrevskiy
  • 23,308
Léo Léopold Hertz 준영
  • 459
  • 1
    A possible track (https://en.wikipedia.org/wiki/N-ellipse) – Jean Marie Mar 19 '17 at 10:52
  • @JeanMarie Is two-foci ellispe enough for this? – Léo Léopold Hertz 준영 Mar 19 '17 at 11:06
  • 1
    No, a classical (2-foci) ellipse has two axis of symmetry, not one as is the case here. – Jean Marie Mar 19 '17 at 12:34
  • 1
    See the answer I gave to a recent similar question (http://math.stackexchange.com/q/2163361) with a Matlab program – Jean Marie Mar 19 '17 at 12:38
  • @JeanMarie Is it then a 3-foci ellipse? Are there any differences in the thread and here? – Léo Léopold Hertz 준영 Mar 19 '17 at 16:12
  • 1
    IMHO, I think that in your problem, having only 3 foci introduces a bias. You could maybe try to have 3+1, (or 4+1), with the group of 3, (or the group of on a regular polygon: equilateral triangle (or square) and take the remaining one on the 3D axis defined by the regular polygon, maybe with a weight equal to 2 (which amounts to say that this last point is in fact two points at the same place). – Jean Marie Mar 19 '17 at 16:21

1 Answers1

1

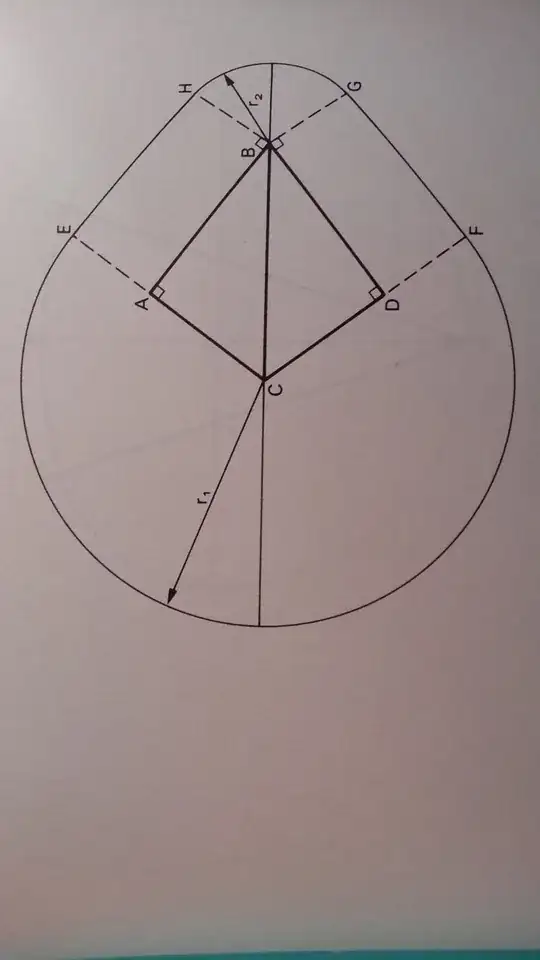
As I see that a part of your "egg" is very linear, here is a little drawing (see below) that may inspire you. It comes from a book of van der Waerden named "Geometry and Algebra in Ancient Civilizations") It is made of circle arcs and straight lines. Of course, it remains to revolve it along its axis of symmetry, getting a portion of sphere, a truncated cone, and a portion of a smaller sphere. enter image description here

Jean Marie
  • 88,997
  • Can you extend the n-elliptical to 3-foci, 4-foci and 5-foci in MATLAB? - - I am thinking how to implement those. I think n-ellipse is not trivial at all. – Léo Léopold Hertz 준영 Mar 19 '17 at 16:49
  • 1
    Why ? What prevents you to add for example a fourth point in (x0,y0,z0) like this ; V = sqrt(X.^2 + Y.^2 + Z.^2)+... sqrt((X-1).^2 + Y.^2 + Z.^2)+... sqrt(X.^2 + (Y+3).^2 + Z.^2)+sqrt(X-x0).^2 + (Y-y0).^2 + (Z-z0).^2) scatter3([0,1,0,x0],[0,0,-3,y0],[0,0,0,z0],10,'b','filled'); ? – Jean Marie Mar 19 '17 at 18:32