6

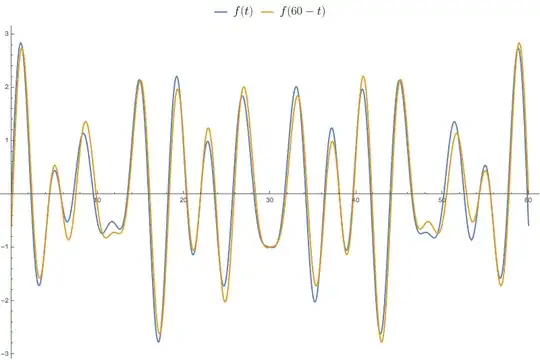
A comment under this answer suggests looking at the graph of $$f(t) = \sin t + \sin(\sqrt 2\ t) + \sin(\sqrt3\ t),$$ and I did so, on the interval $0\le t\le 60.$ I was struck by a seeming near-symmetry, so I let $$g(t) = f(60-t)$$ and superimposed the graphs of $f$ and $g$ on each other and saw how close they are to each other. The correlation between $f$ and $g$ on that interval is more than $0.97.$ Is there some reason for that?

Remark: In one sense the answer is perfectly obvious and is that given by "Reese" below. Yet the fact that such small numbers of half-periods should be so close to each other, although it explains what we see, itself feels as if it calls for explanation.

enter image description here

Martin Sleziak
  • 56,060
Michael Hardy
  • 1
  • MichaelHardy: Since you are the tag creator, I though it might be useful to let you know that there is a post on meta suggesting the removal of the (coincindences) tag: https://math.meta.stackexchange.com/questions/27653/tag-management-2018/28751#28751 – Martin Sleziak Jul 25 '18 at 18:38

1 Answers1

9

$\sqrt{2} \cdot 60$ is almost exactly $27\pi$; $\sqrt{3} \cdot 60$ is almost exactly $33\pi$. And $60$ isn't far from $19\pi$. And conveniently, $\sin(n\pi - x) = \sin(x)$ whenever $n$ is odd. So all three component functions come close to lining up under the transformation $t \to 60 - t$, creating a cool little coincidence when you add them all together.

Reese Johnston
  • 18,258
  • 1
    This is all perfectly obvious, but still it's astonishing, partly because those multiples of the periods are so small. – Michael Hardy Feb 13 '17 at 02:11