4

Consider some $X \sim B(n,p)$. I know that $E[X] = np$.

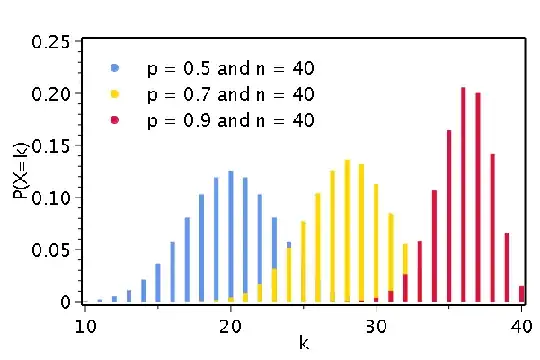
I was looking at practice problems on the binomial distribution. One of the exercises asked the following: Given a histogram and $n$ for some $B(n,p)$, find $p$. (The histograms look like those in the attached image, obviously with $p$ removed.) The solution seems to be to find the value $k$ for which the histogram is maximal (by reading it off the histogram.) Then, $p = \frac{k}{n}$, since apparently $k$ is the expected value.

Obviously, the mean and mode don't coincide for an arbitrary probability distribution. So does this mean that for any $B(n,p)$, the mean and mode are equal?

example histograms

Also: What happens if there are two maxima, like in the figure below?

two maxima

aras
  • 5,757
  • 1
    Roughly yes, but the mean in general is not integer. See here http://math.stackexchange.com/questions/117926/finding-mode-in-binomial-distribution – leonbloy Feb 01 '17 at 11:08
  • 2
    @leonbloy I see. So $\lfloor (n+1)p \rfloor$ is the mode in all cases, and if $np$ happens to be an integer, then (if $p<1$) then both the mean and the mode are $np$. – aras Feb 01 '17 at 11:10

1 Answers1

1

If $p=1/3$ and $n=40$ then $np= 40/3 = 13.33333\ldots,$ and the mode must be an integer.

What do you multiply $\Pr(X=x)$ by to get $\Pr(X=x+1)$?

\begin{align} \frac{\Pr(X=x+1)}{\Pr(X=x)} = \frac{\dbinom n x p^x (1-p)^{n-x}}{\dbinom n {x+1} p^{x+1} (1-p)^{n-x-1}} = \frac{(x+1)(1-p)}{(n-x-1)p} \end{align} This is $<1$ if $x<np-1$ and is $>1$ if $x>np-1.$

Thus $\Pr(X=x+1)>\Pr(X=x)$ when $x<np-1$

and $\Pr(X=x+1)<\Pr(X=x)$ when $x>np-1.$

When $x=np-1$ then there are two modes differing from each other by $1.$

In the concrete example above, $np-1 = 12.33333\ldots,$ so $\Pr(X=12) < \Pr(X=13) > \Pr(X=14),$ so the mode is $13.$

Michael Hardy
  • 1
  • 1
    The fraction given seems to be reciprocal to the formula in the first line. Also, my result doesn't quite line up - I got (n-x)p instead (n-x-1)p (and a quick wolfram query seems to agree with me) – Luke Dec 10 '17 at 22:46