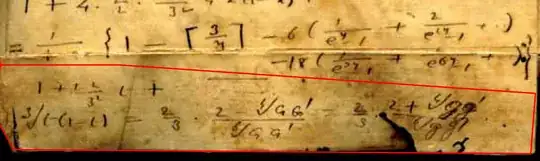Ramanujan's theory "$q_{3}$"
How to calculate singular moduli $t=\alpha_{3,n}$ explicitly of this?
$$\frac{\,_2F_1\big(\tfrac13,\tfrac23,1,1-t\big)}{\,_2F_1\big(\tfrac13,\tfrac23,1,t\big)} =\sqrt{n}$$
Where can I find how to do this? In the Berndt's book "Ramanujan's Notebook, part V" at page 179-180, there is a tentative to explain how
$$\big(t(1-t)\big)^{\frac 1 3}=\frac{2}{3} \frac{2-(G G')^{1/4}} {(G G')^{1/6}}=\frac 2 3 \frac{2+(g g')^{1/4}}{(g g')^{1/6}}$$
using theory "$q_{2}$".
We think to have decrypted the demand equation.
To explain Entry at the buttom of p.25 of the III Ramanujan's Notebook,
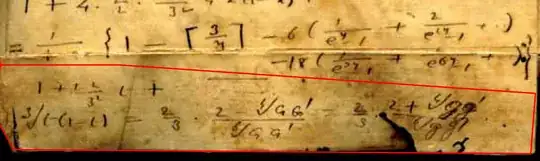we think so:
$$\frac{1}{\big(t(1-t)\big)^{\frac 1 3}}=\frac{2}{3} \frac{2-(G G')^{1/4}} {(G G')^{1/6}}=\frac 2 3 \frac{2+(g g')^{1/4}}{(g g')^{1/6}}$$
where
$t=\beta=\alpha_{3n}$ , $\frac{1}{G}=G_{9n}^{24}$ and $\frac{1}{G'}=(G_{n})^{24}$
while
$\frac{1}{g}=(g_{9n})^{24}$ and $\frac{1}{g'}=(g_{n})^{24}$
$g_{n}$,$G_{n}$ are Ramanujan's functions (Class Invariants).
$$\frac{1}{\big(t(1-t)\big)^{\frac 1 3}}=\frac{2}{3} \frac{2-(G G')^{1/4}} {(G G')^{1/6}}$$
From first Entry of page n. 254 of the Chapter XXI of the II Notebook (page numbering of Ramanujan, that here is shown)
it is clear that
$\beta=\frac{27}{4}\frac{(p+p^{2})^{2}}{(1+p+p^{2})^{3}}$
and the link with $q_{2}$ theory implies that
$\alpha=p^{3}\frac{2+p}{1+2p}$
where $p=\frac{m-1}{2}$ with multiplicator $m$ of degree 3, equal to:
$$m^{2}=1+2 \sqrt{2} \frac{(G_{n})^{3}} {(G_{9n})^{9}}=\frac {9}{1+2\sqrt{2}\frac{(G_{9n})^{3}} {(G_{n})^{9}}}$$
Set
$\rho=\frac{G_{n}}{\sqrt{2}(G_{9n})^{3}}$ and $\tau=\frac{G_{9n}}{\sqrt{2}(G_{n})^{3}}$
then the modular equation of third degree can be written thus:
$$\rho^3=\frac{1-\tau^{3}}{1+8 \tau^{3}}$$
The multiplicator $m$ is: $m^{2}=1+8\rho^{3}$ and although $m=1+2p$, we can write $m^{2}=1+4p+4p^{2}=1+8\rho^{3}$
We have
$p+p^2=2\rho^{3}$.
Then
$$\beta=\frac{27}{4}\frac{(2\rho^{3})^{2}}{(1+2\rho^{3})^3}=\frac{27\rho^{6}}{(1+2\rho^{3})^3}.$$
We need to calculate $(1-\beta)$:
$$(1-\beta)=1-\frac{27\rho^{6}} {(1+2\rho^{3})^3}=\frac{(\rho^{3}-1)^{2}(1+8\rho^{3})} {(1+2\rho^{3})^3}=\frac{27\tau^{6}}{(1+2\tau^{3})^3}$$
Now we observe, always by modular equation of the third degree, that
$$\frac{\tau}{\rho^{2}}+\frac{\rho}{\tau^{2}}=\frac{1}{\rho^{2}\tau^{2}}-8\rho\tau$$.
Then
$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac{1+2\rho^{3}} {3\rho^{2}}\frac{1+2\tau^{3}}{3\tau^{2}}$
$=\frac {2}{9}\big(\frac{1}{2\rho^{2}\tau^{2}}+2\rho\tau+\frac{\tau}{\rho^{2}}+\frac{\rho}{\tau^{2}}\big)$
$=\frac{2}{9}\big(\frac{1}{2\rho^{2}\tau^{2}}+2\rho\tau+\frac{1}{\rho^{2}\tau^{2}}-8\rho\tau\big)$
$=\frac {2}{9}\big(\frac{3}{2\rho^{2}\tau^{2}}-6\rho\tau\big)$
$$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac {2}{3}\big(\frac{1}{2\rho^{2}\tau^{2}}-2\rho\tau\big)$$
With the following substitutions
$\rho\tau=\frac{G_{n}}{\sqrt{2}(G_{9n})^{3}}\frac{G_{9n}}{\sqrt{2}(G_{n})^{3}}=\frac{1}{2(G_{9n})^{2}(G_{n})^{2}}$
$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac{2}{3}\big(2(G_{9n})^{4}(G_{n})^{4}-\frac{1}{(G_{9n})^{2}(G_{n})^{2}}\big)$.
Also we have
$$(G G')^{1/12}=\frac{2}{\rho\tau}=\frac{1}{(G_{9n})^{2}(G_{n})^{2}}$$
At the end we arrive to write
$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac{2}{3}\big(\frac{2}{(G G')^{1/6}}-(G G')^{1/12}\big)=$
$$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac{2}{3} \frac{2-(G G')^{1/4}} {(G G')^{1/6}}$$
Q.E.D.
2.We 'll show the second identity:
$$\frac{1}{\big(t(1-t)\big)^{\frac 1 3}}=\frac 2 3 \frac{2+(g g')^{1/4}}{(g g')^{1/6}}$$
We set
$r=\frac{g_{n}}{\sqrt{2}(g_{9n})^{3}}$
and
$s=\frac{g_{9n}}{\sqrt{2}(g_{n})^{3}}$
we use the modular equation of third degree for $g_{n}$ and $g_{9n}$:
$$1-8r^{3}=\frac{9}{1+8s^{3}}$$
Setting
$m'=1+2p$ and $m'^{2}=1-8r^{3}$,
the value of $p+p^{2}=-2r^{3}$,
moreover the value of singular modulus will be:
$\beta=\frac{27}{4}\frac{(-2r^{3})^{2}}{(1-2r^{3})^{3}}$
that is equal to:
$\beta=\frac{27r^{6}}{(1-2r^{3})^{3}}$
It is necessary to calculate $(1-\beta)$:
$(1-\beta)=1-\frac{27r^{6}}{(1-2r^{3})^{3}}=\frac{(r^{3}+1)^{2}(1-8r^{3})}{(1-2r^{3})^{3}}=\frac{27s^{6}}{(1+2s^{3})^{3}}$
Now we observe by the modular equation of the third degree that
$$\frac{s}{r^{2}}-\frac{r}{s^{2}}=\frac{1}{r^{2}s^{2}}+8rs$$
Thus
$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac{(1-2r^{3})} {3 r^{2}}\frac{(1+2 s^{3})}{3 s^{2}}$
$=\frac {2}{9}\big(\frac{1}{2 r^{2} s^{2}}-2 r s+\frac{s}{r^{2}}-\frac{r}{s^{2}}\big)$
$=\frac{2}{9}\big(\frac{1}{2 r^{2}s^{2}}-2 r s+\frac{1}{r^{2}s^{2}}+8 r s\big)$
$=\frac {2}{9}\big(\frac{3}{2 r^{2}s^{2}}+6 r s\big)$
$$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac {2}{3}\big(\frac{1}{2 r^{2} s^{2}}+2 r s\big)$$
Also we have
$$r s=\frac{g_{n}}{\sqrt{2} (g_{9n})^{3}}\frac{g_9n}{(\sqrt{2}g_{n})^{3}}=\frac{1}{2 (g_{9n}g_{n})^{2}}$$
Moreover
$$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac{2}{3}\big(2(g_{9n}g_{n})^{4}+\frac{1}{(g_{9n}g_{n})^{2}}\big)$$
Also we have
$(g g')^{1/12}=\frac{1}{(g_{9n}g_{n})^{2}}$
making substitution in the last expression we arrive at
$$\frac{1}{\big(\beta(1-\beta)\big)^{1/3}}=\frac {2} {3} \big(\frac{2}{(g g')^{1/6}}+{(g g')^{1/12}}\big)$$
$$=\frac 2 3 \frac{2+(g g')^{1/4}}{(g g')^{1/6}}$$
Q.E.D.
Now the link between $q_{3}$ theory and $q_{2}$ theory:
$$\big(\frac{1} {\alpha_{3n}}\big)^{1/3}=\frac{2}{3} \frac{(G_{9n})^{6}}{(G_{n})^{2}}+\frac{\sqrt{2}}{3} \frac{G_{n}} {(G_{9n})^{3}}$$
$$\big(\frac{1} {\alpha_{3n}}\big)^{1/3}=\frac{2}{3}\frac{(g_{9n})^{6}} {(g_{n})^{2}}-\frac{\sqrt{2}}{3}\frac{g_{n}}{(g_{9n})^{3}}$$
$$\big(\frac{1}{\beta_{3n}}\big)^{1/3}=\frac{2}{3}\frac{(G_{n})^{6}}{(G_{9n})^{2}}+\frac{\sqrt{2}}{3}\frac{G_{9n}}{(G_{n})^{3}}$$
$$\big(\frac{1}{\beta_{3n}}\big)^{1/3}=\frac{2}{3}\frac{(g_{n})^{6}} {(g_{9n})^{2}}+\frac{\sqrt{2}}{3}\frac{g_{9n}}{(g_{n})^{3}}$$
Knowing the invariant values $G_{n}$, $G_{9n}$, $g_{n}$ and $g_{9n}$, we calculated the first ten singular moduli:
$\alpha_{1}=\frac{1}{2}$
$\alpha_{2}=\frac{1}{2}-\frac{\sqrt{2}}{4}$
$\alpha_{3}=\big(\frac{\sqrt{3}-1}{2}\big)^3$
$\alpha_{4}=\frac{9-5\sqrt{3}}{18}$
$\alpha_{5}=\frac{25-11\sqrt{5}}{50}$
$\alpha_{6}=\big(\frac{4-\sqrt{6}}{10}\big)^3$
$\alpha_{7}=\frac{18-13\sqrt{3}+\sqrt{21}}{36}$
$\alpha_{8}=\frac{2-17\sqrt{2}+9\sqrt{6}}{4}$
$\alpha_{9}=\big(\frac{2^{1/3}-1}{2^{1/3}+2}\big)^3$
$\alpha_{10}=\frac{54-35\sqrt{2}-2\sqrt{5}}{108}$
These solve:
$$\frac{\,_2F_1\big(\tfrac13,\tfrac23,1,\,1-\alpha_n\big)}{\,_2F_1\big(\tfrac13,\tfrac23,1,\,\alpha_n\big)} =\sqrt{n}$$
Other applications:
$G_{n}=G_{3}=2^{1/12}$,
$G_{9n}=G_{27}=\frac{2^{1/12}}{(2^{1/3}-1)^{1/3}}$
$$\alpha_{9}=\frac{1+3 2^{1/3}-3 2^{2/3}}{2(2^{2/3}+1)^{3}}=\bigg(\frac{2^{1/3}-1}{2^{1/3}+2}\bigg)^3$$
Given $n=2$, $\alpha_{3n}=\alpha_{6}=?$,
$g_{n}=g_{2}=1$, $g_{9n}=g_{18}=(\sqrt{3}+\sqrt{2})^{1/3}$
$$\frac{1}{(\alpha_{6})^{1/3}}=4+\sqrt{6}$$
Given
$n=\frac{4}{3}$,
$\alpha_{3n}=\alpha_{4}=?$,
$g_{n}=g_{4/3}=2^{1/6}\big(\frac{\sqrt{3}-1}{\sqrt{2}}\big)^{1/4}$,
$g_{9n}=g_{12}=2^{1/6}\big(\frac{\sqrt{3}+1}{\sqrt{2}}\big)^{1/4}$
$$(\frac{1}{\beta_{4}})^{1/3}=\frac{\sqrt{3}(\sqrt{3}-1)}{2^{1/3}}$$
$$\beta_{4}=\frac{1}{2}+\frac{5 \sqrt{3}}{18}.$$
and so on...
This question has a lovely connection to the Monster group. (But Ramanujan didn't know it as that is 1970s maths.)
Let $q = e^{2\pi i\tau}$ and $\tau = \sqrt{-d}$ or $\tau = \frac{1+\sqrt{-d}}2$. Given the Dedekind eta function $\eta(\tau)$, consider the known functions,
\begin{align} j_{1}(\tau) &= \left(\frac{E_4(\tau)}{\eta^8(\tau)}\right)^3 = \frac{1}{q} + 744 + \color{red}{196884}q + 21493760q^2 +\cdots\\ j_{2}(\tau) &=\left(\left(\frac{\eta(\tau)}{\eta(2\tau)}\right)^{12}+2^6 \left(\frac{\eta(2\tau)}{\eta(\tau)}\right)^{12}\right)^2 = \frac{1}{q} + 104 + \color{red}{4372}q + 96256q^2 +\cdots\\ j_{3}(\tau) &=\left(\left(\frac{\eta(\tau)}{\eta(3\tau)}\right)^{6}+3^3 \left(\frac{\eta(3\tau)}{\eta(\tau)}\right)^{6}\right)^2 = \frac{1}{q} + 42 + \color{red}{783}q + 8672q^2 +\cdots\\ j_{4}(\tau)&=\left(\left(\frac{\eta(\tau)}{\eta(4\tau)}\right)^{4}+4^2 \left(\frac{\eta(4\tau)}{\eta(\tau)}\right)^{4}\right)^2 = \left(\frac{\eta^2(2\tau)}{\eta(\tau)\,\eta(4\tau)} \right)^{24} = \frac{1}{q} + 24+ \color{red}{276}q + \dots \end{align}
where $196883, 4371, 782$ (the first three red numbers minus $1$) is the smallest degree $>1$ of the irreducible representations of the Monster group, Baby Monster, and Fischer group $Fi_{23}$, respectively. To find singular moduli $\alpha_n$ for parameters $s = \frac16,\frac14,\frac13,\frac12,$ one unified approach is to solve the quadratic in $\alpha_n$,
$$j_{1}(\tau) = \frac{432}{\alpha_1\,(1-\alpha_1)}$$
$$j_{2}(\tau) = \frac{64}{\alpha_2\,(1-\alpha_2)}$$
$$j_{3}(\tau) = \frac{27}{\alpha_3\,(1-\alpha_3)}$$
$$j_{4}(\tau) = \frac{16}{\alpha_4\,(1-\alpha_4)}$$
yielding the $\alpha_n(\tau)$,
$$ \alpha_1(\tau) = \frac12\left(1-\sqrt{1-\frac{1728}{j_{1}(\tau)}}\right)\qquad\qquad\qquad$$
$$\alpha_2(\tau) = \frac{64}{\left(\frac{\eta(\tau)}{\eta(2\tau)}\right)^{24}+64} = \left(\frac{8}{\left(\frac{\eta(\tau/2)}{\eta(2\tau)}\right)^{8}+8}\right)^2$$
$$\alpha_3(\tau) = \frac{27}{\left(\frac{\eta(\tau)}{\eta(3\tau)}\right)^{12}+27} = \left(\frac{3}{\left(\frac{\eta(\tau/3)}{\eta(3\tau)}\right)^{3}+3}\right)^3$$
$$\alpha_4(\tau) = \frac{16}{\left(\frac{\eta(\tau)}{\eta(4\tau)}\right)^{8}+16} = \left(\frac{\sqrt2\,\eta(\tau)\,\eta^2(4\tau)}{\eta^3(2\tau)}\right)^8$$
For convenience, let $\alpha_n = \alpha_n(\tau)$. Then,
$$\left(\frac{_2F_1\big(\frac16,\frac56,1,\,1-\alpha_1\big)}{_2F_1\big(\frac16,\frac56,1,\,\alpha_1\big)}\right)^2=-1\,\tau^2$$
$$\left(\frac{_2F_1\big(\frac14,\frac34,1,\,1-\alpha_2\big)}{_2F_1\big(\frac14,\frac34,1,\,\alpha_2\big)}\right)^2=-2\,\tau^2$$
$$\left(\frac{_2F_1\big(\frac13,\frac23,1,\,1-\alpha_3\big)}{_2F_1\big(\frac13,\frac23,1,\,\alpha_3\big)}\right)^2=-3\,\tau^2$$
$$\left(\frac{_2F_1\big(\frac12,\frac12,1,\,1-\alpha_4\big)}{_2F_1\big(\frac12,\frac12,1,\,\alpha_4\big)}\right)^2=-4\,\tau^2$$
If $\tau=\sqrt{-n/4}=\frac12\sqrt{-n}$, then the last is the well-known,
$$\frac{K'(k)}{K(k)} = \sqrt{n}$$
with complete elliptic integral of the first kind $K(k).\,$ So $\alpha_4\big(\tfrac{\tau}2\big)$ in fact is the square of the elliptic modulus $k$ and is also the modular lambda function $\lambda(\tau)$,
$$\alpha_4\big(\tfrac{\tau}2\big) = k^2 = \lambda(\tau) = \left(\frac{\sqrt2\,\eta\big(\tfrac{\tau}2\big)\,\eta^2(2\tau)}{\eta^3(\tau)}\right)^8 $$
If $\tau=\sqrt{-n/3}$, then we have the second-to-the-last,
$$\frac{_2F_1\big(\frac13,\frac23,1,\,1-\alpha_3\big)}{_2F_1\big(\frac13,\frac23,1,\,\alpha_3\big)}=\sqrt{n}$$
which is the desired equation in the original post.