5

Integral is the summation of continuous numbers. Taking for example the graph for $y=x$ for $x$ between $[0,2]$, the area/integral is $2$. Now if I take summation for discrete $y=x$, $x \in \mathbb{Z}$ between $[0,2]$, the summation is 3.

What I'm wondering is how the summation over continuous terms (which does include the discrete terms) is less than the summation over discrete terms?

Did
  • 284,245
akipro
  • 123
  • "Continuous summation" would be $\displaystyle\sum_{x\in[0,2]}x$ which is infinite. – Guest Jan 09 '17 at 07:39
  • Is integral not continuous summation? Am I wrong in saying that? – akipro Jan 09 '17 at 07:40
  • Define what you mean by "continuous summation". The Riemann integral is a limiting process. – Guest Jan 09 '17 at 07:41
  • what do we actually mean when we say, "integral (from a to b) xdx "? Please pardon me if it is a too trivial question. I get your point that since there are infinite terms between [0,2] the sum will be infinite. Integral is usually taught as the sum of numbers in a range (similar to the idea of sum of finite discrete n numbers) – akipro Jan 09 '17 at 07:49
  • It is the limit (in a very precise manner) to which particular finite sums tend to. See here. – Guest Jan 09 '17 at 07:52

2 Answers2

7

Thinking of integral as sum of continuous numbers is unsound at best, and your question is a good example of why. Instead, a better comparison can be made with sum of areas of rectangles of a certain width (say, w) whose heights match the function (i.e. x). The smaller the width of the bars, the closer to the integral you get. They both become equal as the width of the bars becomes infinitesimally small.

Let me try to illustrate this with a few of pictures. Firstly, here's a picture representing your example. The sum of integers is represented by yellow bars of width 1, while the integral is represented by the green area.

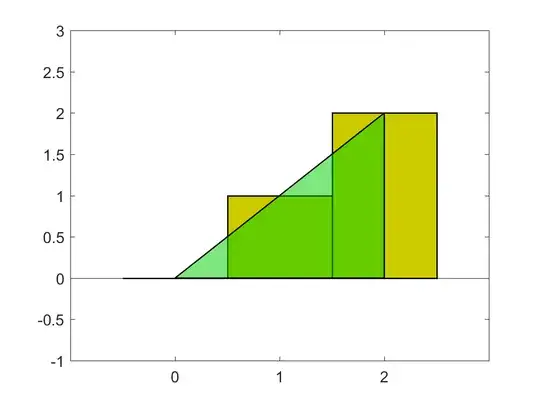coarse sum You can see that the sum of bars has an extra rectangular space, of height 2 and width 0.5, at the very right. That's why your sum is 1 more than the integral.

A better approximation can be made if we reduced the width of the bars. For example, in the following picture, w = 0.25: 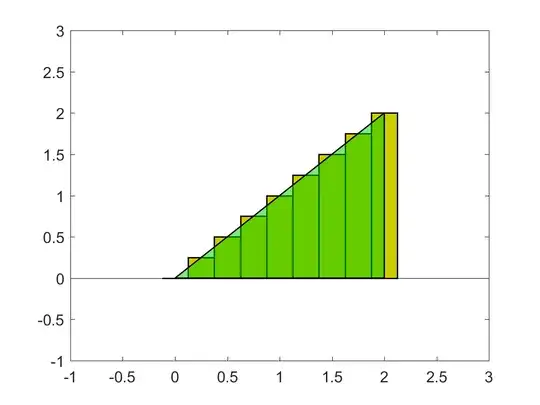fine sum Clearly, the area of the bars is now closer to the actual integral than the previous example. The same trend continues as you keep making the bars narrower, ultimately converging exactly to the integral as w tends to 0.

aksadv
  • 196
1

As already pointed out by aksadv and the comments, sums and integrals produce similar results, but are different concepts that have to be evaluated differently. That said, the similarity of their results is often exploited by using simple integrals to approximate difficult sums and vice versa.

For instance, $\sum_{n=1}^N n^k$ is a difficult sum, but $\int_1^N x^k \, dx$ is quite simple, so using the integral and the Euler-Maclaurin Summation Formula which characterizes the difference between the two, we can find an exact formula for the sum.

CodeLabMaster
  • 763