4

I created a random number generator (numbers from 0-100 exclusive) and was looking for a way to test for randomness, is there a statistical test that would help me with this and how would I use it?

BruceET
  • 52,418
Matt B
  • 41
  • 1
    You could just use a chi square test and test whether your randomly generated numbers (of some chosen sample size,make sure it's large enough and look at the assumptions for the chi square) ) follows a uniform distribution – Brandon Jan 02 '17 at 23:27
  • 1
    How big a sample do you expect? With a sample of size $30$ I might approach this differently from the way I would with a sample of $10{,}000. \qquad$ – Michael Hardy Jan 03 '17 at 00:34

1 Answers1

1

Here are some issues to consider in vetting a pseudorandom number generator.

1) Tests for uniform distribution. The Kolmogorov-Smirnov test is one possibility if you are emulating a continuous uniform distribution. In R statistical software, here is how to generate 1000 values intended to be distributed as $Unif(0,1)$ and subsequent testing to see if they are:

x = runif(1000, 0, 1)
ks.test(x, "punif", 0, 1)

    One-sample Kolmogorov-Smirnov test

data:  x 
D = 0.0321, p-value = 0.2547
alternative hypothesis: two-sided

Because the P-value exceeds .05, the 1000 pseudorandom numbers in the vector x are consistent with a random sample of size 1000 from $Unif(0,1).$

However, this test is for continuous data and does not handle tied observations. If you are generating integers between 0 and 100, then you might do a chi-squared goodness-of-fit test as Commented by @Brandon. If you have a sample of fewer than 5000, I would suggest collapsing the data into a few categories, perhaps nine: 1-11, 12-22, etc.

2) Length of period. Many PRNGs repeat their output in the same sequence after producing a certain number of values (called the period of the generator). Your generator will not be useful for most practical applications if its period is too short.

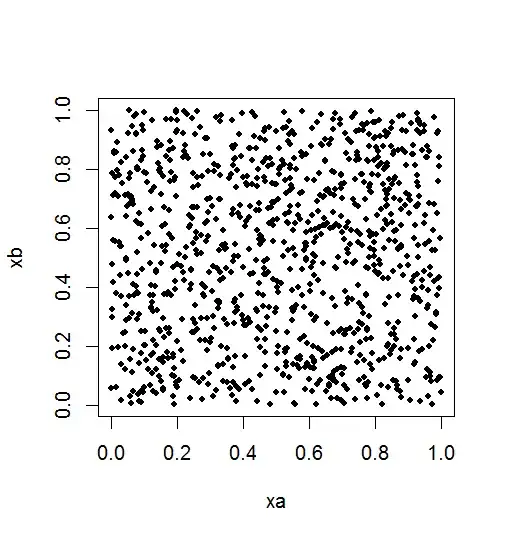
3) Look at 2-D plots. If you have a sequence of 1000 numbers $X_1, \dots, X_{1000},$ you can plot the vector $(X_1, \dots, X_{999})$ against $(X_2, \dots, X_{1000}).$ The points should 'fill' the unit square uniformly and with no noticeable pattern.

 xa = x[1:999];  xb = x[2:1000]
 plot(xa, xb, pch=20)

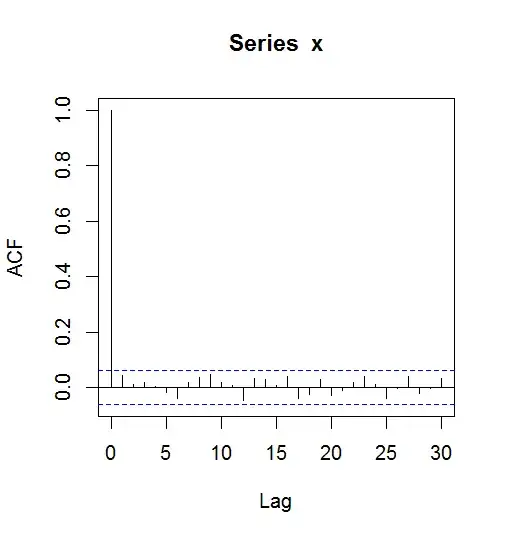
enter image description here

You also want the numbers to be free of patterns in higher dimensions. One method to check for certain kinds of patterns in higher dimensions is the 'autocorrelation plot', which should show no significant autocorrelations with various lags. [Vectors xa and xb above are lagged by one index.] For the vector x generated in R, there no lags up to 30 with significant autocorrelations (straying beyond the dotted boundaries in the plot). The line at the far left is for lag-0 and so has correlation $r=1.$

acf(x)

enter image description here

(4) Batteries of benchmark tests. Making useful PRNGs is a tricky business. At this point we do not know how to give a set of rules that will guarantee success. But there are batteries of tests that have shown previous generators to be flawed. For example, you can read about 'Marsaglia's Die-Hard' battery of tests on Wikipedia.

Note: One of the best PRNGs in use today is the 'Mersenne twister'. It has an extremely long period, has been checked for patterns in high dimensions, and has passed many benchmark tests. It is the default generator in R. You can read about it in the Wikipedia article or elsewhere on the Internet.

BruceET
  • 52,418