6

I am aware of a few analytical calculations showing that the stereographic projection sends circles on the sphere to circles on the equatorial plane. There are related questions here.

What about a geometrical proof? I have found one somewhere that goes as follows.

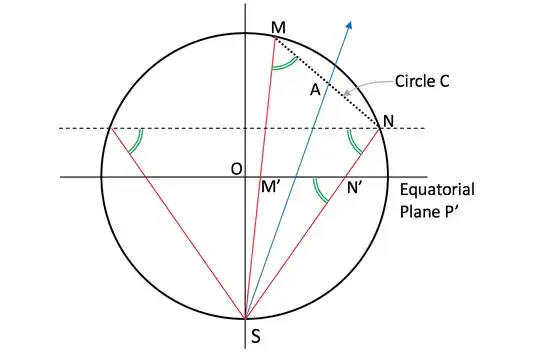
Let $O$ be the center of the sphere and $S$ the pole doing the projection. Choose a circle $C$ on the sphere lying on a plane $P$, and denote its center $A$. The rays joining $S$ to the circle $C$ cross the equatorial plane $P'$ at some points, which we want to prove form another circle. Let $M$ and $N$ be the two points on the circle $C$ such that they belong to the $SOA$ plane. Their stereographic projection on the equatorial plane are denoted by $M'$ and $N'$.

enter image description here

The angles noted in the attached figure can easily be proven equal, leading to the two angles $SMN$ and $SN'M'$ being equal. This means that the planes $P$ and $P'$ are symmetrical to each other by reflection across the axis $SA$ (shown as an arrow). Now, the proof follows saying that the "cone" from $S$ to $C$ has the same symmetry, so that its intersections with the two planes $P$ and $P'$ are "equivalent". As a consequence, the two intersections are circles, and this proves the theorem.

But wait. To me, this is not really a "cone". But fine, it does not need to be. However, it does not seem symmetrical across $SA$: taking the symmetric point of $N$ or $M$ will clearly not land on the same "cone". So that would mean that the two shapes made by intersecting with $P$ and $P'$ should not be equivalent; consequently, stereographic projection would not send circles to circles.

Where is my error?

Community
  • 1
fffred
  • 304
  • 1
  • 9
  • 1
    there is a proof by picture in Hilbert and Cohn-Vossen, Geometry and the Imagination. I will see if I can find the correct pictures on line. Alright, mostly pages 248-251 – Will Jagy Dec 30 '16 at 00:58
  • can't have everything; they do not show page 250, but do 248, 249, 251 https://books.google.com/books?id=7WY5AAAAQBAJ&pg=PA251&lpg=PA251&dq=hilbert+cohn-vossen+stereographic+projection+and+circle-preserving&source=bl&ots=EblPIVuYmY&sig=ItVCyPwLkK7EPwL_-Q-tIWSg6B0&hl=en&sa=X&ved=0ahUKEwjZtNCs3JrRAhUN6WMKHfYpDvQQ6AEIHDAA#v=onepage&q=hilbert%20cohn-vossen%20stereographic%20projection%20and%20circle-preserving&f=false – Will Jagy Dec 30 '16 at 01:05
  • 1
    Are you aware that, by sterographic projection, the image of the center is not the center of the image ? Said otherwise, the centers of the circle on the sphere and the center of the corresponding circle on the equatorial plane are (generally) not aligned with $S$. – Jean Marie Dec 30 '16 at 20:41
  • @JeanMarie, I did not know, but what does it change for this question? – fffred Dec 31 '16 at 17:26
  • It was just a remark, without direct incidence on the question. – Jean Marie Dec 31 '16 at 18:33
  • An answer to your problem may be found here: https://www.math.ubc.ca/~cass/research/pdf/Stereographic.pdf Peter – Peter Ells Jul 10 '18 at 11:11

2 Answers2

5

The cone is perhaps an oblique one, but it is a cone we are looking at: based on the circle $C$ from plane $P$, with summit $S$.
(Note however, that being oblique only means, from other perspective, that it's a straight cone based on another conic section.)

Now the main point is that - as seen in current picture - the plane $P'$ meets this cone in the same angle as $P$ does. So the conic section of $P'$ will be similar to that of $P$, so will be a circle.

The wording is not too lucky: I guess the symmetry is about the cone itself.

Berci
  • 92,013
  • I can accept that this definition of a cone, but I still don't see that symmetry in this case. The angles might be the same for the two planes, but they are on opposite sides of the cone, so that a symmetry is required. You say that it is a straight cone: what does this mean? Does it imply its symmetry across an axis? – fffred Dec 30 '16 at 10:46
  • @fffred: The sphere is symmetric "front to back" (i.e., in the plane of your diagram), so the cone has elliptical cross-sections in planes orthogonal to its axis $SA$, and one axis of these ellipses is perpendicular to the plane of the diagram. The relevant symmetry is, as you say, reflection in $SA$ (i.e., reflection in the plane perpendicular to the plane of the diagram and containing $SA$); the cone is preserved because its cross sections are ellipses, and the reflection plane bisects each along an axis. – Andrew D. Hwang Mar 06 '17 at 12:03
  • I like this argument, and I am trying to clarify it to myself. Perhaps like this: we are dealing with a cone, and it has an obvious plane of symmetry passing through the vertex. It will necessarily have another plane of symmetry passing through the vertex. Now we reflect the circle section in that plane and get another circle section. – orangeskid Dec 14 '21 at 05:04
0

I also had the same doubts about this proof and I came out with two solutions:

  1. Better understand the symmetry argument. The difficulty is that we do not know explicitly which symmetry convinces us that the the section of the "cone" (the oblique one projected from $S$ to circle $C$) lying on the equatorial plane is also a circle. @fffred told you already one symmetry: the reflection about the plane $A$ through the angle bisector. But, certainly you don't get one circle from the other only by applying this reflection. The solution is that you need one homothety from $S$ to complete the transformation: First, start with your circle $C$ and reflect it about $A$ to get $C_1$. Notice $C_1$ has the same diameter as $C$. Second, make an homothety through $S$ from $C_1$ to $C_2$ which is a circle whose plane intersects the segment $M'N'$ at the same point as the angle bisector. Also, the diameter of circle $C_2$ is the length of line segment $M'N'$. Notice that this circle $C_2$ is precisely $C'$. PD: You get the same result if you apply the homothety first and then the reflection.
  2. Make an explicit metric argument that convinces you that the projection of $C$ is a circle. Imagine $X$ a point lying on circle $C$ and $X'$ a point lying on $C'$ and both points are above the plane of the screen. Let's call the projections onto the plane of the screen $Y$ and $Y'$ and set that $S$, $Y$, and $Y'$ are collinear. If under these assumptions we can prove that $S$, $X$, and $X'$ are collinear then we will be done. Define $h$ the distance from $X$ to the plane of the screen, and analogously define $h'$ with $X'$. The desired collinearity will be proved iff $\frac{h}{h'}=\frac{|SY|}{|SY'|}$ (think about the two similar right triangles $SXY$ and $SX'Y'$ that would be formed). To complete the proof you need the intersecting chord theorem twice to see $h^2=|MY|\cdot |NY|$ and $h'^2=|M'Y'|\cdot |N'Y'|$. Also, you need to apply the law of sines four times to see that $|SY|^2=\frac{|MY|\cdot |NY|\sin\alpha\sin\beta}{\sin\gamma\sin\delta}$ and $|SY'|^2=\frac{|M'Y'|\cdot |N'Y'|\sin\alpha\sin\beta}{\sin\gamma\sin\delta}$. I'll leave the details regarding which angles are those $\alpha$, $\beta$, $\gamma$, and $\delta$.
olaphus
  • 151