15

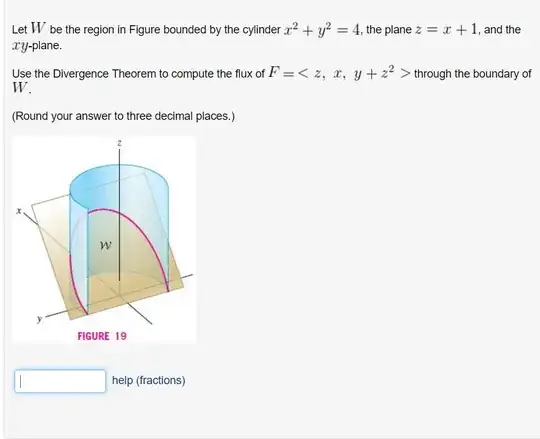
image

Let $W$ be the region bounded by the cylinder $x^2+y^2=4$, the plane $z=x+1$, and the $xy$-plane. Use the Divergence Theorem to compute the flux of $F = \langle z,x,y+z^2 \rangle$ through the boundary of $W$.

So far I've gotten to the point of computing div$(F)$ and integrating from $0$ to $x+1$ to obtain $$\iint_{D}(x+1)^2 dA.$$

My problem is finding the bounds of the domain which is the circle of radius $2$ centered at the origin. I understand I must use polar coordinates but since the circle is cut off by the line $x=-1$ I'm having trouble figuring out what the bounds for the radius should be. I think $\theta$ goes from $2\pi/3$ to $4\pi/3$ (somewhat guessing the bound for theta when the radius is cut off by the line $x = -1$)

Dr.Antidode
  • 423
Hendrix
  • 1,466
  • 1
  • 11
  • 20

2 Answers2

7

The divergence theorem allows us to write $$ \iint_S\vec{F}\cdot d\vec{S}=\iiint_W \nabla\cdot \vec{F}\; dV = \iiint_W 2z\; dV $$ where $W$ is the region bounded by $x^2+y^2=4$, $z=x+1$ and $z=0$, i.e., $$ W=\{(x,y,z)\;|\; -1\le x \le 2,\; 0\le z\le 1+x,\; -\sqrt{4-x^2}\le y \le \sqrt{4-x^2} \} $$ It follows that $$ \iiint_W 2z\; dV = \int_{-1}^2\int_0^{1+x}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}2z\; dydzdx = \int_{-1}^2\int_0^{1+x} 4z\sqrt{4-x^2}\; dzdx \\= \int_{-1}^22(1+x)^2\sqrt{4-x^2}\; dx = \frac{16\pi}{3}+\frac{9\sqrt{3}}{2} $$

Kuifje
  • 9,802
1

If $x = r\cos\theta = -1$, then \begin{align*} r = -\frac{1}{\cos\theta} = -\sec\theta \end{align*} But since this means you will eventually have two compute two integrals, maybe polar coordinates is not the way to go. \begin{align*} \iint_D (x+1)^2\,dA &= \int_{-1}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(x+1)^2\,dy \,dx \\ &= 2 \int_{-1}^2 (x+1)^2\sqrt{4-x^2}\,dx \\ \end{align*} Then substitute $x=2\sin\theta$.

Matthew Leingang
  • 27,777