Notational conventions Question $\to$ Answer : $(x_0,y_0,z_0) \to (x,y,z)$ , $\lambda_0 \to (\xi,\eta,\zeta)$ .
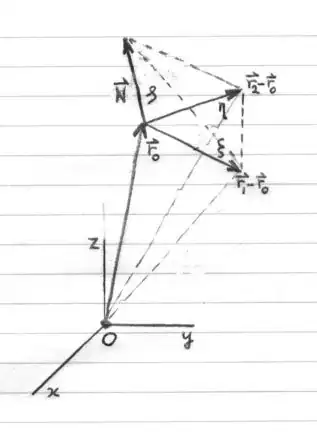
See picture. Instead of a planar triangle, consider a prism with a triangle from the triangular mesh as the base.
Let this triangle be spanned by the vectors $(\vec{r}_1-\vec{r}_0)$ and $(\vec{r}_2-\vec{r}_0)$. In addition, define the
normal at the triangle by the cross product $\;\vec{N} = (\vec{r}_1-\vec{r}_0)\times(\vec{r}_2-\vec{r}_0)$ . Now we can establish
the (isoparametric) transformation / barycentric coordinates $(\xi,\eta,\zeta)$ :
$$
\vec{r}-\vec{r}_0 = (\vec{r}_1-\vec{r}_0)\xi + (\vec{r}_2-\vec{r}_0)\eta + \vec{N}\zeta
$$
Writing out in components $\vec{r} = (x,y,z)$ gives three equations with three unknowns $(\xi,\eta,\zeta)$ . So:
$$
\begin{bmatrix} \xi \\ \eta \\ \zeta \end{bmatrix} =
\begin{bmatrix}
x_1-x_0 & x_2-x_0 & (y_1-y_0)(z_2-z_0)-(z_1-z_0)(y_2-y_0) \\
y_1-y_0 & y_2-y_0 & (z_1-z_0)(x_2-x_0)-(x_1-x_0)(z_2-z_0) \\
z_1-z_0 & z_2-z_0 & (x_1-x_0)(y_2-y_0)-(y_1-y_0)(x_2-x_0) \end{bmatrix}^{-1}
\begin{bmatrix} x-x_0 \\ y-y_0 \\ z-z_0 \end{bmatrix}
$$
Solving these enables any position $\vec{r}$ at the Riemann surface be expressed into $(\xi,\eta,\zeta)$.
Here $\zeta\vec{N}$ is a measure for the distance between the triangle considered and the point $\vec{r}$ at the Riemann surface.
Once this distance small enough, the parameters $(\xi,\eta)$ determine whether the point $\vec{r}$ is inside or outside the
triangle, in the plane with normal $\vec{N}$ : it is inside when $0 < \xi < 1$ and $0 < \eta < 1$ and $\xi+\eta < 1$ , outside when anything else. If inside, then evaluate the function, expressing it in values at the triangle vertices:
$$
u = u_0 + (u_1-u_0)\xi + (u_2-u_0)\eta
$$
Gradient of the function $u$ in a few steps.
Chain rules for partial derivatives:
$$
\begin{cases} \Large
\frac{\partial u}{\partial \xi} =
\frac{\partial u}{\partial x}\frac{\partial x}{\partial \xi} +
\frac{\partial u}{\partial y}\frac{\partial y}{\partial \xi} +
\frac{\partial u}{\partial z}\frac{\partial z}{\partial \xi} \\ \Large
\frac{\partial u}{\partial \eta} =
\frac{\partial u}{\partial x}\frac{\partial x}{\partial \eta} +
\frac{\partial u}{\partial y}\frac{\partial y}{\partial \eta} +
\frac{\partial u}{\partial z}\frac{\partial z}{\partial \eta} \\ \Large
\frac{\partial u}{\partial \zeta} =
\frac{\partial u}{\partial x}\frac{\partial x}{\partial \zeta} +
\frac{\partial u}{\partial y}\frac{\partial y}{\partial \zeta} +
\frac{\partial u}{\partial z}\frac{\partial z}{\partial \zeta}
\end{cases}
$$
In matrix form:
$$\Large
\begin{bmatrix} \frac{\partial u}{\partial \xi} \\ \frac{\partial u}{\partial \eta} \\ \frac{\partial u}{\partial \zeta} \end{bmatrix} =
\begin{bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} & \frac{\partial z}{\partial \xi} \\
\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} & \frac{\partial z}{\partial \eta} \\
\frac{\partial x}{\partial \zeta} & \frac{\partial y}{\partial \zeta} & \frac{\partial z}{\partial \zeta}
\end{bmatrix}
\begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial u}{\partial z} \end{bmatrix}
$$
Inverse:
$$ \Large
\begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial u}{\partial z} \end{bmatrix} =
\begin{bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} & \frac{\partial z}{\partial \xi} \\
\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} & \frac{\partial z}{\partial \eta} \\
\frac{\partial x}{\partial \zeta} & \frac{\partial y}{\partial \zeta} & \frac{\partial z}{\partial \zeta}
\end{bmatrix}^{-1}
\begin{bmatrix} \frac{\partial u}{\partial \xi} \\ \frac{\partial u}{\partial \eta} \\ \frac{\partial u}{\partial \zeta} \end{bmatrix}
$$
Transpose:
$$ \Large
\begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial u}{\partial z} \end{bmatrix} =
\begin{bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} & \frac{\partial x}{\partial \zeta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} & \frac{\partial y}{\partial \zeta} \\
\frac{\partial z}{\partial \xi} & \frac{\partial z}{\partial \eta} & \frac{\partial z}{\partial \zeta}
\end{bmatrix}^{-T}
\begin{bmatrix} \frac{\partial u}{\partial \xi} \\ \frac{\partial u}{\partial \eta} \\ \frac{\partial u}{\partial \zeta} \end{bmatrix}
$$
Where did we see this matrix before?
$$
\begin{bmatrix} \partial u/\partial x \\ \partial u/\partial y \\ \partial u/\partial z \end{bmatrix} =
\begin{bmatrix}
x_1-x_0 & x_2-x_0 & (y_1-y_0)(z_2-z_0)-(z_1-z_0)(y_2-y_0) \\
y_1-y_0 & y_2-y_0 & (z_1-z_0)(x_2-x_0)-(x_1-x_0)(z_2-z_0) \\
z_1-z_0 & z_2-z_0 & (x_1-x_0)(y_2-y_0)-(y_1-y_0)(x_2-x_0) \end{bmatrix}^{-T}
\begin{bmatrix} u_1-u_0 \\ u_2-u_0 \\ 0 \end{bmatrix}
$$
