2

I am currently studying the PageRank algorithm. To find the ranks i know you have two options:

  • Compute the result of a large linear system
  • Apply the surfer concept (like Markov chains)

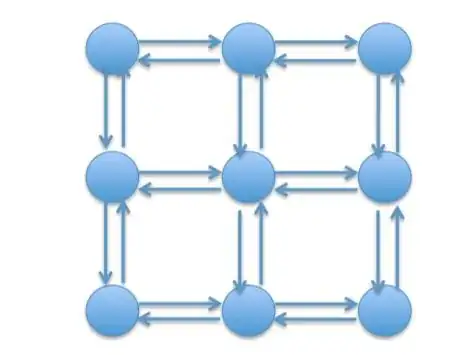
I have this graph below, is a grid composed of 3x3 nodes. The central node has more connections so I guess it will have more rank than the others, the nodes 2,4,6,8 have 3 incomming connections and the others have incomming degree 2. enter image description here

Can I assume that the nodes 1,3,7,9 have the same pageRank values? Also for 2,4,6,8? What is the best way to compute the PageRank for this graph? Thanks, very much.

Marc Ortiz
  • 145

1 Answers1

2

Due to symmetry, you know that $2,4,6,8$ will have the same rank (call it $r_s$, as in side), and $1,3, 7,9$ will also have the same rank (call it $r_c$, as in corner). The central node has its own rank, call it $r_0$

Now, look at the equations that $r_s$ must satisfy. Since $r_s=r_2$, you can look at the equation for $r_2$, and it is $r_2 = \frac14 r_0 + \frac12 r_1 + \frac12 r_3$ which translates in our new variables into $$r_s = \frac14 r_0 + \frac12 r_c + \frac12 r_c$$

Next, the equation for $r_1$ is $r_1 = \frac{1}{3}r_2 + \frac13 r_4$ which translates into

$$r_c = \frac13 r_s + \frac13 r_s$$

Finally, the equation for $r_0$ translates from $r_0=\frac13 r_2 + \frac13 r_4 + \frac13 r_6 + \frac13 r_8$ into $$r_0=\frac13 r_s + \frac13 r_s + \frac13 r_s + \frac13 r_s$$

Simplifying, you now have a system of $3$ equations with $3$ variables:

$$r_s = \frac14 r_0 + r_c\\ r_c = \frac23 r_s\\ r_0 = \frac43 r_s$$

which shoudln't be hard to solve at all.

5xum
  • 126,227
  • 6
  • 135
  • 211