44

My brother in law and I were discussing the four color theorem; neither of us are huge math geeks, but we both like a challenge, and tonight we were discussing the four color theorem and if there were a way to disprove it.

After some time scribbling on the back of an envelope and about an hour of trial-and-error attempts in Sumopaint, I can't seem to come up with a pattern that only uses four colors for this "map". Can anyone find a way (algorithmically or via trial and error) to color it so it fits the four color theorem?

"five color" graph

Doktor J
  • 671
  • 85
    They call it the Four Color Theorem for a reason – you can't disprove it. – Gerry Myerson Nov 02 '16 at 06:31
  • If you start colouring from the centre, it may not work well. I suggest that you start colouring the outer shell. – edm Nov 02 '16 at 06:31
  • 14
    I love how people go "I can't think of it therefore counterproof of what has been proven to always be true" – Zelos Malum Nov 02 '16 at 06:38
  • 3
    I tried to colour the graph in several ways, and it seems that there is only one way (up to isomorphism) to colour the graph. – edm Nov 02 '16 at 06:46
  • 33
    @GerryMyerson Right, because no proof of a theorem, especially one with such a controversial history using the one of the most controversial proof techniques in all of mathematics, has ever been wrong. – sloth Nov 02 '16 at 07:29
  • 18
    @sloth, how much would you like to bet that the Four Color Theorem isn't wrong? – Gerry Myerson Nov 02 '16 at 08:01
  • 47
    @sloth the computerised check of the four-colour system may have been controversial when it was published, as it was just some program that could well have had bugs in it. But it has since been backed up by a dependently-typed proof system. You can't get any more certain than that about any proof. – leftaroundabout Nov 02 '16 at 10:53
  • I seem to remember that quite early there was a proof that any map with 39 or fewer colours could be four-coloured. Long before there was any claim of a proof for the full theorem. – gnasher729 Nov 02 '16 at 14:10
  • 13
    @ZelosMalum I never said "I can't think of it therefore counterproof". I had a strong suspicion it could be done, which is why I posted it here -- I wanted help breaking my so-called counterproof and figured a fresh set of eyes could probably crack it in a matter of minutes where I had gotten myself into a methodological rut. – Doktor J Nov 02 '16 at 19:22
  • 4
    @gnasher729 that can't be right, because it is a simple theorem that any planar map can be 5-colored – Anton Fetisov Nov 02 '16 at 20:41
  • 2
    @ZelosMalum OP went from "I can't think of it" to asking about it in a math forum. Sounds perfectly fine to me. – djechlin Nov 02 '16 at 21:32
  • A proof was published in 1880 but a fatal flaw was found in about 1890. The length of the delay may have been due to a lack of interest in the Q, and a vastly smaller population of mathematicians compared to today. – DanielWainfleet Nov 03 '16 at 02:48
  • I read about this in school. The 3-color theorem can be proven mathematically but the 4-color theorem was only proven recently (recently when I was in school) by a combination of mathematical paper and a massive computer program that did a brute force search. So in short, this is a really hard problem to do, and if you do it, you can write your Master's about it. (except that someone already did) – RDS_JAF Nov 02 '16 at 20:58
  • @RDS_JAF Sorry if this makes you feel old, but it was proved in like 1977. I think for a combinatorics theorem that's old enough that you should no longer call it "recently". – Zsbán Ambrus Nov 02 '16 at 21:17
  • 29
    The rule of thumb is to always assume that you are the one missing something. You should never say "a possible disproof" (or rather "counterexample"), but rather "What am I missing here? I am probably wrong." Sure, people have made mistakes in the past. People have claimed to have proved something, only years later to learn of subtle mistakes that they have made. But courtesy to *the rest of the mathematical community* dictates that you should generally assume that the fault lies in your understanding, rather than with everyone else. Which is why your post has come under fire here. – Asaf Karagila Nov 03 '16 at 09:27
  • 1
    @DoktorJ Your post is headed 'disproof'. If that's not what you're asking, change it. – user207421 Nov 03 '16 at 19:08
  • 1
    @user254665: I think the problem was that the 1880 proof basically gave an algorithm how to turn a five colouring into a four colouring. A good software developer of today would look at that algorithm and say "wait a second, this looks dodgy, I'm not convinced that it works", think about it for an hour, and find an example where it doesn't work. It's a different mindset. – gnasher729 Nov 03 '16 at 21:40
  • 1
    http://www-history.mcs.st-and.ac.uk/HistTopics/The_four_colour_theorem.html - "Franklin in 1922 published further examples of unavoidable sets and used Birkhoff's idea of reducibility to prove, among other results, that any map with ≤ 25 regions can be 4-coloured. The number of regions which resulted in a 4-colourable map was slowly increased. Reynolds increased it to 27 in 1926, Winn to 35 in 1940, Ore and Stemple to 39 in 1970 and Mayer to 95 in 1976." So the "counterexample" was disproven in 1922. – gnasher729 Nov 03 '16 at 21:48
  • @gnasher729 According to the book Mathematical Recreations and Essays by Rousse-Ball and Coxeter, the flaw in the 1880 proof was the assumption that a connected trivalent graph (Every node lying on exactly 3 edges) cannot have an isthmus (An edge which,if removed, disconnects the graph.) The book also gives a simple counter-example. – DanielWainfleet Nov 03 '16 at 21:54
  • 1
    There is a mathematical proof to the problem. It was done by Dr. Appel and Dr. Haken. https://en.wikipedia.org/wiki/Four_color_theorem – Alan Nov 03 '16 at 21:57
  • 5
    @DoktorJ: I believe your intent in asking this question was fine, asking the community for help in finding out what was wrong with your supposed counterproof. But the "disproof" in the title, even with a question mark, was a little bit provocative. Some math people are touchy. – LarsH Nov 03 '16 at 23:49
  • This trick may be useful: http://math.stackexchange.com/questions/1911474/on-the-four-and-five-color-theorems – DVD Nov 10 '16 at 22:29

6 Answers6

121

Starting at the top, going clockwise:

  • center: 1, 2, 3
  • middle: 2,4,3,4,2,4
  • outside: 1

4colors

I hope this helps $\ddot\smile$

dtldarek
  • 37,969
  • 6
    Accepting this one because it was first, and works. I knew my brother-in-law and I couldn't have broken something like this in a one hour brainstorming session at 2am, LOL – Doktor J Nov 02 '16 at 14:27
  • 4
    Not only is it correct, but I think every four-coloring of this map can be obtained from this one by some sequence of rotation, reflection, or swapping colors (for example, rotate $120$ degrees, then reflect through the vertical line through the center, then swap the red and blue colors, then swap the blue and green colors). – David K Nov 02 '16 at 14:58
  • 19
    +1 for having a relatively color blind friendly coloring. At least compared to other colorings on this page. – Asaf Karagila Nov 02 '16 at 23:15
  • 12
    I can imagine Google using that design for one of their products. – camden_kid Nov 03 '16 at 17:09
  • @DavidK: I noticed the same thing about all the answers here. Do you have an idea of a proof? – tomasz Nov 03 '16 at 21:40
  • @tomasz My ideas were: The three inner circle colors must be distinct. Prove by contradiction that the outer ring color must be one of those three colors. Rotate the map so the inner-circle color matching the outer ring is uppermost. Show that all other colors except the top segment of the middle ring then are determined. Show there are two choices for the top segment's color; choose one. By reflecting the map through the vertical axis (or not reflecting it) make the lower left middle-ring segment match the top segment. Then swap colors until they match the map above. – David K Nov 03 '16 at 22:40
  • @DavidK: That sounds like it should work. Thanks. – tomasz Nov 04 '16 at 00:08
  • @tomasz I just noticed that Tanner Swett gave an answer yesterday that follows basically the same line of argument. – David K Nov 04 '16 at 01:51
47

A few people have commented that all of the answers given so far have been identical up to symmetry (either by exchanging colors, or by using a symmetry of the uncolored diagram). Here's a proof that the answer that everyone has given is the only possible answer, up to symmetry.

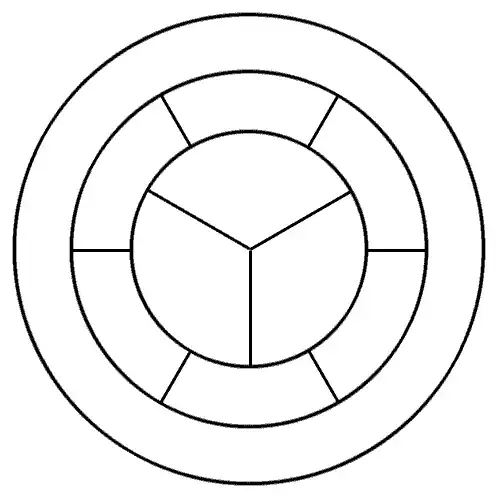
Let me number the regions, like so:

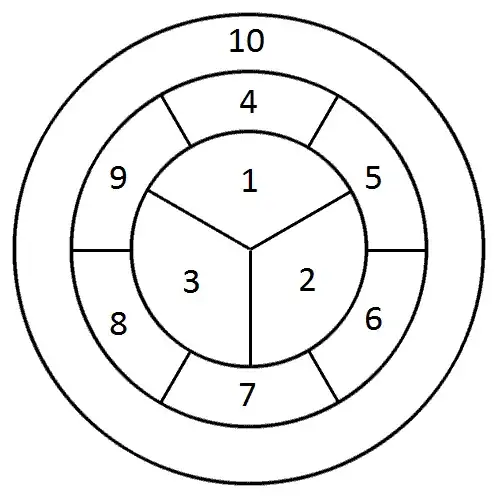
Numbered map

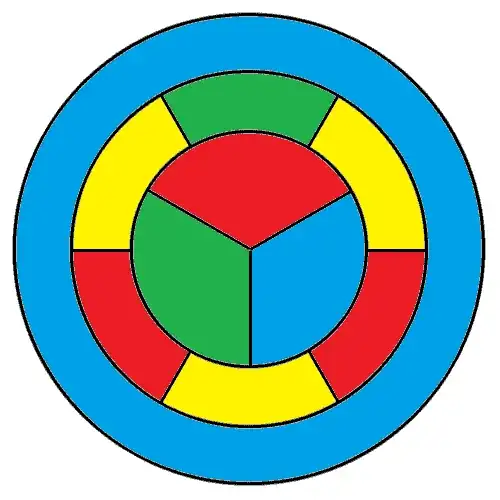
Without loss of generality, assume that region 1 is red, region 2 is green, and region 3 is blue.

Is region 10 yellow? I will prove that it is not. Suppose that region 10 is yellow. Then since region 5 borders regions 1 (red), 2 (green), and 10 (yellow), region 5 must be blue. Next, since region 6 borders regions 2 (green), 5 (blue), and 10 (yellow), region 6 must be red. Now region 7 borders regions 2 (green), 3 (blue), 6 (red), and 10 (yellow), so it cannot be colored. This proves that region 10 is not yellow.

We now know that region 10 must be red, green, or blue. Without loss of generality, assume that region 10 is red.

Now we can find:

  • Region 7 borders regions 2 (green), 3 (blue), and 10 (red). Therefore, region 7 is yellow.
  • Region 6 borders regions 2 (green), 7 (yellow), and 10 (red). Therefore, region 6 is blue.
  • Region 5 borders regions 1 (red), 2 (green), 6 (blue), and 10 (red). Therefore, region 5 is yellow.
  • Region 8 borders regions 3 (blue), 7 (yellow), and 10 (red). Therefore, region 8 is green.
  • Region 9 borders regions 1 (red), 3 (blue), 8 (green), and 10 (red). Therefore, region 9 is yellow.

At this point, the only uncolored region is region 4. Its neighbors are regions 1 (red), 5 (yellow), 9 (yellow), and 10 (red). We can complete the coloring by choosing either green or blue. Both choices will give the same coloring, up to symmetry.

Sophie Swett
  • 10,830
  • Nice work. FWIW, using Knuth's AlgorithmX with the first 3 colours fixed as per your answer, I get these solutions: RGBGYRYRYB, RGBGYRYGYB, RGBGYBYGYR, RGBBYRYRYG, RGBBYBYRYG, RGBBYBYGYR; in numeric form that's 0121303032, 0121303132, 0121323130, 0122303031, 0122323031, 0122323130. – PM 2Ring Nov 03 '16 at 14:26
33

This works, as you can check..

enter image description here

Arkya
  • 628
29

Although I wouldn't call it an algorithm, you can construct a solution equivalent to those of the other three answers via this rational approach:

  1. Assign a color C1 to the outer ring. It's a promising candidate because of the symmetry and topology of the figure.

  2. Observe that

    • the outer ring has no boundary in common with the inner disk, so C1 can be re-used there
    • each region of the inner disk borders the other two, so these three regions must each have a distinct color

  3. Therefore choose two more colors C2 and C3, and assign C1, C2, and C3 as the colors of the regions of the inner disk. It doesn't matter which color is assigned to which region, as all arrangements are interconvertible by symmetry operations on the figure, as partially colored in step (1).

  4. Observe that there is exactly one segment of the middle ring that borders both C2 and C3 from the inner disk; it also, perforce, borders C1 from the outer ring. That segment requires a fourth color, C4.

  5. The color assignments made to this point leave only one choice each (without using a fifth color) for the remaining middle-ring segments other than the one opposite the region assigned in the previous step. Having made those assignments, two alternatives remain for the final region; either can be assigned.

PellMel
  • 391
21

One possible 4-coloring of such.

enter image description here

dxiv
  • 77,867
6

To answer the "algorithmically" question, this map has some regions that only border four others. There is a relatively short, algorithmic proof that if you can 4-colour all but one of the regions of a map, and the last region, R, only borders four others (call them R_1, R_2, R_3, R_4 in clockwise ordering about R), then you can colour the whole map. To do this, work as follows. It is easy unless R_1 to R_4 already use all the colours. Say they are blue, green, red, yellow in that order around region R. Now we try to recolour R_1 to red, in the hope that this will allow us to colour R blue. If we do that, we have to recolour any red region which borders R_1 blue. Then we have to recolour any blue region which borders one of these red, and so on. We keep doing this until we run out of things to recolour. Now one of two things happens: either we can colour R blue or we had to recolour R_3 blue. In the latter case, there was a chain of red and blue regions stretching from R_1 to R_3, but there can't also be a chain of green and yellow regions stretching from R_2 to R_4 (they have to cross somewhere, but the fact that they use different colours means that they can't). So now if we try the same trick recolouring R_2 yellow, any yellow regions next to R_2 green, and so on, this time we won't have to recolour R_4, and we will be able to colour R green.

We've now shown that if we can colour everything apart from a region that meets four (or fewer) others, we can do this recolouring trick and then colour the last region. Similarly, if we had a colouring of some of the regions, and one of the uncoloured regions only bordered four coloured ones, we can recolour in this way and then colour that region as well. So if we can find an ordering of regions such that each one borders at most four previous ones, we can progressively recolour in this way. In this map we can -- basically progressively remove regions that only have four neighbours in what's left, then reverse that ordering -- so this algorithm will work.

This method was the basis of Kempe's incorrect proof of the 4-colour theorem, and was used by Heawood to prove the 5-colour theorem (using five colours we are ok so long as there is always a region we can remove which borders at most five others, but that is true for any plane map). It can be used to easily find a 4-colouring of Martin Gardner's "April Fools" map, which would be very difficult to find by trial and error.

Especially Lime
  • 46,692