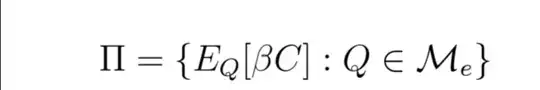Relative entropy for martingale measures

Question

I need some help understanding a note given in a lot of papers I've read.

Let $(\Omega,\mathcal{F},P)$ be a complete probability Space, $\mathbb{F} = (\mathcal{F}_t)_{t\in[0,T]}$ a given filtration with usual conditions, $S$ be a locally bounded semi-martingale and $$M_a = \{ Q \ll P \; | \; S \text{ is a locale } (Q,\mathbb{F})-\text{martingale}\}$$ the set of all absolutely continuous martingale measures.

Now I found a lot of papers claiming it's natural to assume that the set $$M_e = \{ Q \in M_a \; | \; H[Q|P] < +\infty \}$$

is non empty where

$$H[Q|P] = \begin{cases} E_P\Big[\frac{dQ}{dP}\log\frac{dQ}{dP}\Big] & \mbox{ if }Q \ll P \\ +\infty & \mbox{ otherwise} \end{cases} $$

is the relative entropy of $Q$ w.r.t $P$.

But I see no reason why $M_e \not= \emptyset$ should hold.

Maybe someone has a hint or link for me.

edit 09.12.2019: To point out my main issue here (see comments to second answer): It's totally clear to me why the set $M_a$ of absolutely continuous (locale) martingale measures is not empty if we have an arbitrage free (in the NFLVR sense) market. But why does at least one of these measures have a finite entropy related to our initial measure $P$?

Greetings

Answer 1

$M_e$ contains $P$, because $P\in M_a$ and $\frac{dP}{dP}=1$ and therefore $H[P|P]=0.$

I will show that $M_e$ contains more than just $P$ in the case where $S$ is a Brownian motion. In that case, Girsanov's theorem tells us that the elements in $M_a$ are the probability measures $Q$ under which $S$ is a Brownian motion with an added continuous drift $b$, and that $\frac{dQ}{dP}$ satisfies $\frac{dQ}{dP}=D_T$, where \begin{equation*} D_t = \exp\bigg( \int^t_0b(u)dS_u - \tfrac{1}{2}\int^t_0 b(u)^2 du \bigg) \end{equation*} for any $t\in[0,T]$, under the condition that $D$ is a martingale. One sufficient condition that $D$ is a martingale is the Novikov condition, which requires that \begin{equation*} E_P\bigg[\exp\bigg(\tfrac{1}{2}\int^T_0 b(u)^2 du\bigg)\bigg]<\infty. \end{equation*} If $D$ is a martingale, then substitution of $\frac{dQ}{dP}$ in the relative entropy yields \begin{equation*} \begin{split} E_P\bigg[\frac{dQ}{dP}\log\frac{dQ}{dP}\bigg] = E_Q\bigg[\log\frac{dQ}{dP}\bigg] &= E_Q\bigg[\int^T_0 b(u)dS_u\bigg] - E_Q\bigg[\tfrac{1}{2}\int^T_0 b(u)^2 du\bigg] \\ &= E_P\bigg[\int^T_0 b(u)dS_u\bigg] + E_Q\bigg[\tfrac{1}{2}\int^T_0 b(u)^2 du\bigg] \end{split} \end{equation*} (note in the last equality the one change of measure from $Q$ to $P$) where it is used that $S$ is a Brownian motion plus drift $b$ on $(\Omega,\mathcal{F},Q)$. If $b$ satisfies \begin{equation*} E_Q\bigg[\int^T_0 b(u)^2 du\bigg]<\infty, \end{equation*} then the stochastic integral $\int^T_0 b(u)dS_u$ will have zero expectation, and it follows that $H[Q|P]$ is finite.

You might find the following article interesting: http://jbierkens.nl/pubs/2014-scl.pdf It considers the above in more detail and in the context of control theory, where the drift $b$ acts as a control and $H[Q|P]$ as a control cost.

Answer 2

In general S is a P-semi martingale but not a P-local martingale, so in general $P∉M_a.$

A local martingale is a martingale if and only if it is of class (DL)

But I see no reason why $M_e≠∅$ should hold

Usually we consider the set non empty by assumption; moreover, the set $M_e$ is not, in general, a singleton, so we are typically left with

Edit:

This is always stated but as mentioned in my question it was said to be "natural". For me this means that somehow there is a justification why this should hold. Do you have one?

Yes, it is reasonable to make such an assumption, and the justification is quite practical: here is a pic from the book Mathematical Finance - Bachelier Congress 2000 (selected Papers from the First World Congress of the Bachelier Finance Society, Paris, June 29-July 1, 2000), p. 430

Edit (II): I found this, maybe can help:

Moreover,

However, I leave here the link, where the topic is analyzed in more detail: https://projecteuclid.org/download/pdf_1/euclid.aop/1029867119

---

Edit 10-12-2019

(source: http://cfmar2017.pstat.ucsb.edu/talks/Frittelli.pdf)

But we already know this, so the question is

why does at least one of these measures have a finite entropy related to our initial measure P?

This abstract is taken from a paper by Marco Frittelli: The Minimal Entropy Martingale Measure and the Valuation Problem in Incomplete Markets. I've not explored the rest of the article, so I'm not sure whether Frittelli explains or not the reasons you are looking for. Nevertheless, if you are interested here is the paper: http://www.mat.unimi.it/users/frittelli/pdf/EntropyMF2000.pdf