Example: LP Formulation of TSP
Consider the following distance-matrix of 4-Cities TSP:

Exclude the the Diagonal Variables ($X_{11}, X_{22}, X_{33}, X_{44}$) from the Distance Table as shown above via zeros.
The following table represents the Assignment Model + the Additional Constraints resulting from $u_i – u_j + nx_{ij} \le n-1$; where $i,j = 2, \cdots, n$ and i ≠ j.
When n = 4, then,
$$u_i– u_j + nx_{ij} \le 3; \text{ where } i,j = 2, . ., n \text{ and } i ≠ j$$
Then,
$$4x_{23} + u_2 – u_3 \le 3, (i = 2, j = 3)$$
$$4x_{24} + u_2 – u_4 \le 3, (i = 2, j = 4)$$
$$4x_{32} + u_3 – u_2 \le 3, (i = 3, j = 2)$$
$$4x_{34} + u_3 – u_4 \le 3, (i = 3, j = 4)$$
$$4x_{42} + u_4 – u_2 \le 3, (i = 4, j = 2)$$
$$4x_{43} + u_4 – u_3 \le 3, (i = 4, j = 3)$$
V’s X12 X13 X14 X21 X23 X24 X31 X32 X34 X41 X42 X43 U2 U3 U4
1 1 1 1 = 1
2 1 1 1 = 1
3 1 1 1 = 1
4 1 1 1 = 1
5 1 1 1 = 1
6 1 1 = 1
7 1 1 1 = 1
8 1 1 1 = 1
9 4 1 -1 ≤ 3
10 4 1 -1 ≤ 3
11 1 -1 1 ≤ 3
12 1 1 -1 ≤ 3
13 4 -1 1 ≤ 3
14 1 -1 1 ≤ 3
OF 13 21 26 10 29 20 30 20 5 12 30 7
The associated LP consists of the Assignment Model + the Additional Constraints.
$$\text{Minimize } z = 13X_{12} + 21X_{13} + 26X_{14} + 10X_{21} + 29X_{23} + 20X_{24} + 30X_{31} + 20X_{32} + 5X_{34} + 12X_{41} + 30X_{42} + 7X_{43}$$
Subject to:
$$X_{12} + X_{13} + X_{14} = 1$$
$$X_{21} + X_{23} + X_{24} = 1$$
$$X_{31} + X_{32} + X_{34} = 1$$
$$X_{41} + X_{42} + X_{43} = 1$$
$$X_{21} + X_{31} + X_{41} = 1$$
$$X_{12} + X_{32} + X_{42} = 1$$
$$X_{13} + X_{23} + X_{43} = 1$$
$$X_{14} + X_{24} + X_{34} = 1$$
$$4X_{23} + U_2 - U_3 \le 3$$
$$4X_{24} + U_2 - U_4 \le 3$$
$$4X_{32} - U_2 + U_3 \le 3$$
$$4X_{34} + U_3 - U_4 \le 3$$
$$4X_{42} - U_2 + U_4 \le 3$$
$$4X_{43} - U_3 + U_4 \le 3$$
$$U_2, U_3, U_4 \in \Bbb Z^{+}$$
$$x_{ij} \in \{0,1\}, \text{ }\forall ij \in [1,4]$$
Solution Summary for LP of TSP:
Decision Solution Unit Cost or
Variable Value Profit C(j)
1 X12 1.0000 13.0000
2 X13 0 21.0000
3 X14 0 26.0000
4 X21 0 10.0000
5 X23 1.0000 29.0000
6 X24 0 20.0000
7 X31 0 30.0000
8 X32 0 20.0000
9 X34 1.0000 5.0000
10 X41 1.0000 12.0000
11 X42 0 30.0000
12 X43 0 7.0000
13 U2 0 0
14 U3 1.0000 0
15 U4 2.0000 0
Objective Function (Min.) = 59.0000
Therefore, the route is:
$$X_{12} – X_{23} – X_{34} – X_{41} = 59$$
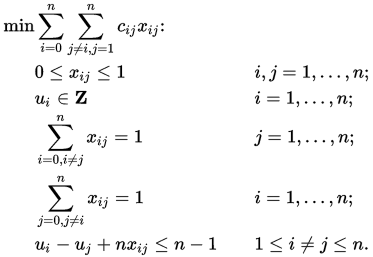



iandj? – Nyxynyx Oct 06 '16 at 23:04Duoduoduosuggested changing the appearance of0to1, while based onLesser Cartographiesdiscussion, I needtto be1because I am interested in the traditional Traveling Salesman Problem where he visits every other city only once. Is the fix for the current formulations to add the sixth constraints involving thetvariable and settto1? – Nyxynyx Oct 06 '16 at 23:10t == 1, which index ranges foriandjshould be used? And are therencities orn+1cities? – Nyxynyx Oct 07 '16 at 01:26