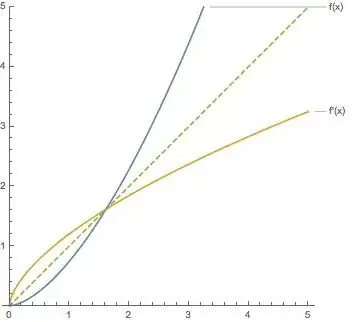
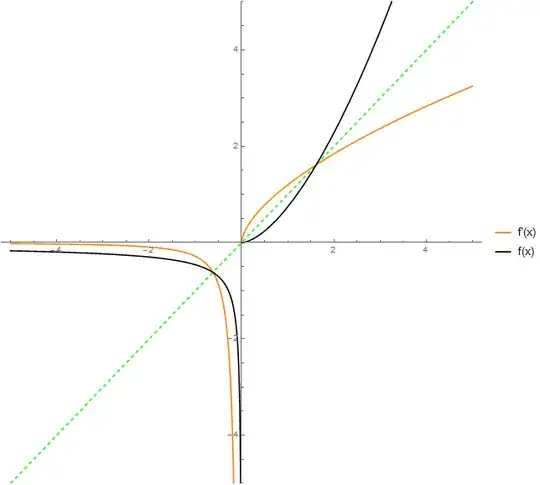
Let's say $f:D\to R$ is an injective function on some domain where it is also differentiable. For a real function, i.e. $D\subset\mathbb R, R\subset\mathbb R$, is it possible that $f'(x)\equiv f^{-1}(x)$?
Intuitively speaking, I suspect that this is not possible, but I can't provide a reasonable proof since I know very little nothing about functional analysis. Can anyone provide a (counter)example or prove that such function does not exist?