Number of positive unequal integer solutions of $x+y+z+w=20$

Question

What is the number of positive different integer solutions of $x+y+z+w=20$, where $x,y,z,w$ are all different and positive?

It would be nice if coding is not used. I am given the answer $552$.

Answer 1

HINT: Each solution of the desired type is a permutation of a solution in which $x<y<z<w$, and every permutation of such an increasing solution is of the desired type. Each increasing solution has $4!=24$ permutations, so you need only count the increasing solutions and multiply by $24$.

Added: This can be done fairly easily by brute force. For other methods see this question. To see what Marc van Leeuwen is doing in his answer, note that

$$\begin{align*} \frac1{1-x}&=1+x+x^2+x^3+\ldots=\sum_{n\ge 0}x^n\\ \frac1{1-x^2}&=1+x^2+x^4+x^6+\ldots=\sum_{n\ge 0}x^{2n}\\ \frac1{1-x^3}&=1+x^3+x^6+x^9+\ldots=\sum_{n\ge 0}x^{3n}\\ \frac1{1-x^4}&=1+x^4+x^8+x^{12}+\ldots=\sum_{n\ge 0}x^{4n} \end{align*}$$

If you take the product of these, each term in that product (before you collect like terms) will be of the form

$$x^{k_1}x^{2k_2}x^{3k_3}x^{4k_4}=x^{k_1+2k_2+3k_3+4k_4}\tag{1}$$

for some non-negative integers $k_1,k_2,k_3$, and $k_4$. When you combine like powers of $x$, the coefficient of $x^{10}$ will be the number of terms like $(1)$ in which $k_1+2k_2+3k_3+4k_4=10$. Finally, there is a bijection between such $4$-tuples $\langle k_1,k_2,k_3,k_4\rangle$ and partitions of $10$ into parts of sizes $1,2,3$, or $4$: $k_i$ is the number of parts of size $i$. And as Marc had already briefly explained, the number of such partitions is equal to the number that we want. You may find it helpful to look at this Wikipedia article; when Marc talks about Young diagrams, he’s talking about what the article calls Ferrers diagrams.

Answer 2

By inclusion-exclusion over the distinctness conditions:

There are $\binom{20-1}3=\binom{19}3$ solutions disregarding the conditions.

There are $\binom42$ ways to choose one pair that fails to be distinct, with common value $k$, and $19-2k$ options for the remaining two values, for a total of

\begin{align} \sum_{k=1}^9(19-2k)&=9\cdot19-2\cdot\frac{9(9+1)}2\\ &=81\;. \end{align}

There are $3$ ways to choose two non-overlapping pairs that fail to be distinct, and $\binom{10-1}1=9$ options for their values, and $12$ ways to choose two overlapping pairs that fail to be distinct, so that three values are equal, and then $6$ different options for the values.

There are $\binom{\binom42}3=\binom63$ ways to choose three pairs, of which $4$ constrain only $3$ values to be equal, leading to $6$ options as above, and the remaining $\binom63-4$ constrain all $4$ values to be equal, leaving only $1$ option.

For $k=4,5,6$, there are $\binom{\binom42}k=\binom6k$ ways to choose $k$ pairs, all of which constrain all $4$ values to be equal and thus leave only $1$ option.

Thus by inclusion-exclusion the total count is

$$ \binom{19}3-\binom42\cdot81+3\cdot9+12\cdot6-4\cdot6-\left(\binom63-4\right)+\binom64-\binom65+\binom66=552\;. $$

Answer 3

Just for comparison with Brian Scott's solution, here is the longhand count solution.

As is observed in several places above, it is sufficient to find the number of solutions with $x<y<z<w$ and multiply by 24, because each such solution can be permuted to give 24 solutions to the original question.

Next note that $1+2+3+4=10$ is the smallest total for 4 unequal positive integers, so we are not going to get many solutions. Now $4+5+6+7>20$, so $x=1,2$ or 3. Since $3+4+5+6=18$ the only possible solutions for $x=3$ are $(3,4,6,7),(3,4,5,8)$.

Similarly for $x=2$ we must have $y=3,4$ or 5. $y=5$ gives only $(2,5,6,7)$. $y=4$ gives only $(2,4,6,8),(2,4,5,9)$. $y=3$ gives only $(2,3,4,11),(2,3,5,10),(2,3,6,9),(2,3,7,8)$.

Finally in a similar way $x=1$ implies $y=2,3,4,5$ and gives solutions $(1,2,3,4),(1,2,4,13),(1,2,5,12),(1,2,6,11),(1,2,7,10),(1,2,8,9)$ and $(1,3,4,12),(1,3,5,11),(1,3,6,10),(1,3,7,9)$ and $(1,4,5,10),(1,4,6,9),(1,4,7,8)$, and $(1,5,6,8)$.

Total 23, hence 552 to question.

--------- shorter version ------

I have spelt this out in full detail, but note that since only the count is required setting out all those cases with $z+w=k$ is not really needed. It is enough to say something like:

$x=3$ implies $y=4$ and 2 solutions

$x=2$ implies: $y=3$, 4 solutions; or $y=4$, 2 solutions; or $y=5$, 1 solution

$x=1$ implies: $y=2$, 6 solutions; or $y=3$, 4 solutions; or $y=4$, 3 solutions; or $y=5$, 1 solution.

Total 23 solutions. Times 4! gives 552 to the original question.

----------- comment ----------

Teachers often give simple questions for you to practice methods like generating functions. But simple questions can often be answered faster by more elementary methods. Often fastest is best!

Answer 4

Here is the best Solution I found when I was preparing for IIT-JEE 2000-2003. suppose equation is $x + y +z + t = N$ find $k= [(N-2n-4)/2]$, where n is the least integer present is the solution. for example to find number of solutions in which least number present is $1$, put $n=1$. Now draw the following diagram 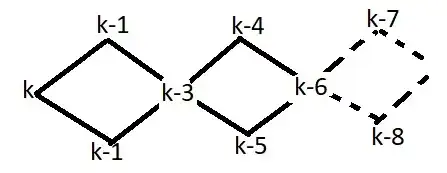Stop when $1$ comes. Now If $N$ is even add lower row terms along with middle row terms and multiply the sum with $4!$. This is the number of unequal integral solution of above equation having n as the least integer. If $N$ is odd add upper row terms along with middle row terms and multiply the sum with $4!$. Repeat the process for other possible values of $N$. In above case $n$ can have values $0, 1, 2$, & $3$, if we are interested in finding non-negative unequal integral solutions, because $4 + 5 + 6 + 7 > 20$ for $n=0$, there are $24\times 4!$ solution for $n=1$, there are $14\times 4!$ solutions for $n=2$, there are $7\times 4!$ solutions and for $n=3$, there are $2\times 4!$ solutions. Total number of non-negative solutions can be obtained by adding all$= 1128$ If you are interested in only positive unequal integral solutions drop the case of n=0, and you get $552$ If you wish to obtain solution for $x, y, z, t > 1$, drop the case $n=0$ and $n=1$ both, and you get $216$. and so on.......