Find the equation of a circle with radius 4 units, whose Centre lies on the line $4x+13y=32$ and which touches the line $4x+3y+28=0$.
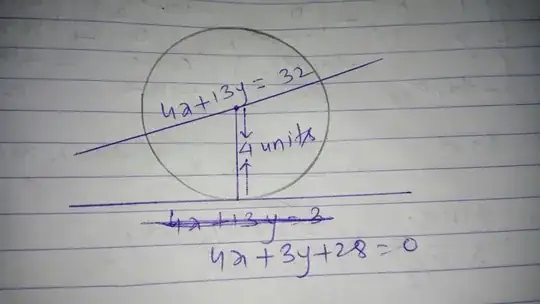
I could only make a figure with the help of the question. can anyone help me to complete this?
Find the equation of a circle with radius 4 units, whose Centre lies on the line $4x+13y=32$ and which touches the line $4x+3y+28=0$.
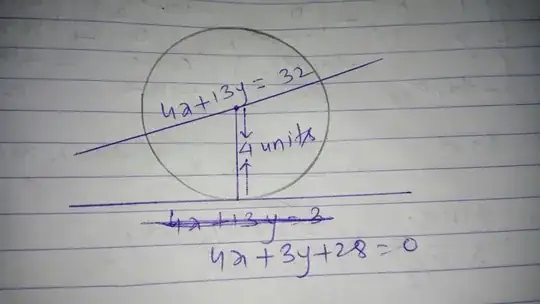
I could only make a figure with the help of the question. can anyone help me to complete this?
$$13y=4(8-x)$$
If $8-x=13h\iff x=8-13h\iff y=4h$
So WLOG, the coordinate of the center can be written as $(8-13h,4h)$
Now the distance of the center from the tangent $=$ radius
$$\implies4=\dfrac{|4(8-13h)+3(4h)+28|}{\sqrt{4^2+3^2}}$$
Can you complete the square & take the problem home from here?
Lab's solution is clever. It may be helpful to explain a bit more his thinking.
The equation $4x+13y=32$ is a line, as you already see, and it has infinitely many points that satisfy it.
Since there are two variables and one equation, there is $2-1=1$ free parameter (which is called $h$ in Lab's solution). Expressing the line in terms of this free parameter is a matter of getting the two variables on opposite sides, and then equating them to the free parameter.
The way it's done in Lab's solution may seem a bit like magic but he sees where he wants to go, and doesn't want to deal with fractions until he has to.
First the equation is rearranged to $13y = 32 - 4x = 4(8-x)$. He sees the opportunity to set $8-x = 13h$ (which he can do at this point). Isolating $x$ gives $x = 8 - 13h$. Upon substituting it there, he has $13y = 4 \cdot 13h$, which gives $y=4h$.
Why do all of this? Because now the line is completely described with one variable, $h$, and the values of $x,y$ can be calculated from $h$. Now it's just a matter of applying the distance formula for a distance $d$ from a point $(x_0, y_0)$ to the line $ax+by+c=0$:
$$d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2+b^2}}.$$
Here, $(x_0, y_0)$ is a point on your parameterized line, which is $(8-13h, 4h)$.
Hope this helps!