10

During 6.042, the students are sitting in an $n$ × $n$ grid. A sudden outbreak of beaver flu (a rare variant of bird flu that lasts forever; symptoms include yearning for problem sets and craving for ice cream study sessions) causes some students to get infected. Here is an example where $n = 6$ and infected students are marked ×.

Example.

Now the infection begins to spread every minute (in discrete time-steps). Two students are considered adjacent if they share an edge (i.e., front, back, left or right, but NOT diagonal); thus, each student is adjacent to $2, 3,$ or $4$ others. A student is infected in the next time step if either:

  • the student was previously infected (since beaver flu lasts forever), or
  • the student is adjacent to at least two already-infected students.

In the example, the infection spreads as shown below.

Example.

In this example, over the next few time-steps, all the students in class become infected.

Theorem. If fewer than $n$ students in class are initially infected, the whole class will never be completely infected.

Prove this theorem.

Hint: When one wants to understand how a system such as the above “evolves” over time, it is usually a good strategy to (1) identify an appropriate property of the system at the initial stage, and (2) prove, by induction on the number of time-steps, that the property is preserved at every time-step. So look for a property (of the set of infected students) that remains invariant as time proceeds.

Source: MIT OCW Mathematics for Computer Science, Problem Set 2, Problem 3.

I am not really sure of how I can prove this. I went out on a limb and assumed that I would be using induction since this seems like a problem that requires an invariant to be used to prove the theorem.

Another thing that I have realized is that if $k$ students are initially infected, then the perimeter of the figure formed by the infected students as the infection spread is at most $4k$. So, this might be my invariant.

So, this is what I have thus far:

Theorem: If fewer than $n$ students in class are initially infected, the whole class will never be completely infected.

Proof: by induction

I would appreciate any and all hints that would help me get the ball rolling with this proof.

Cherry_Developer
  • 4,617
  • since the infection rule "straightens" the infected area (it cannot spread like a "finger" to the uninfected area since you need 2 neighbors and not one) i would try to go backwards from a state where all are infected, dig some "holes" and try to find a state that cannot have a different predecessor (with less than $n$ $\times$). – Max Jun 17 '16 at 09:07
  • 2
    the worst-case-start-condition seems to be the diagonal infected. – Max Jun 17 '16 at 09:11
  • @Max
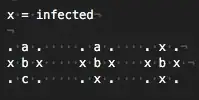
    the worst-case-start-condition seems to be the diagonal infected? Can you elaborate? For example, if I have a $4$ x $4$ grid with x's going down the main diagonal, I will be able to get to a state in which the infection spread completely. So, I am unsure of what you are hinting at here.     – Cherry_Developer Jun 17 '16 at 09:36
  • Yes, the diagonal will spread. But if a single row is infected, the infection will not spread. However, you are not asked to discuss $n$ initial cases. Clearly some spread and some not. You are asked about $<n$ initial cases. – almagest Jun 17 '16 at 09:43
  • This is a version of #34 in the book by Bela Bollobas, The Art of Mathematics: Coffee Time in Memphis. It's also a duplicate of http://math.stackexchange.com/questions/1007373/the-disease-problem – Gerry Myerson Jan 22 '17 at 12:40

3 Answers3

9

You solved your own problem! Consider the length of the boundary. If there are $<n$ infected squares initially, then the length is at most $4(n-1)$. It cannot increase, but if we end up with all squares infected the boundary would be length $4n$.

In the diagram below consider what happens when square $b$ becomes infected. In the first case we get new boundary above and below it (because $a,c$ are uninfected), but we lose the boundary on either side of $b$, so there is no net change.

In the second case, we have a net loss of 2 (we lose three sides of boundary and only gain 1). In the third case we have a net loss of 4.

So in all cases, we cannot increase the total length of boundary - we must lose at least 2 and can gain at most 2.

enter image description here

almagest
  • 18,650
  • Ah. ok. It took me a minute to see what you meant in the second part "[Consider a square with 2 or more infected squares adjacent. When it becomes infected we add at most 2 to the boundary (its sides not adjacent to an infected square) and lose at least 2, so the length of boundary cannot increase.]", but I think I have the hang of it now. So, for example, if we have the row [x][ ][x][ ] from a 4 x 4 grid, then in the state [x][ ][x][ ], we have a perimeter of $8$. Then, I add the infected student to get: [x][x][x][ ]. Now the perimeter is still $8$. I added 2 non adjacent sides, but I took – Cherry_Developer Jun 17 '16 at 10:12
  • away $2$ sides in the process. – Cherry_Developer Jun 17 '16 at 10:12
  • 1
    Or indeed the boundary can decrease. I will add a diagram to make it clearer. – almagest Jun 17 '16 at 10:14
  • Thank you for that diagram. It cleared up quite a bit for me. How would I proceed from here in order to take all of these ideas and turn it into a proof? I take it that I was correct to assume that this will require a proof by induction, yes? – Cherry_Developer Jun 17 '16 at 15:52
  • 1
    It is only induction in a trivial sense. At each time step the length of the boundary cannot increase. But if the infection spreads to all students the boundary ends up at $4n$, so it cannot have started $<4n$. But if it starts with $<n$ students the maximum possible boundary is $4(n-1)$. That is a perfectly rigorous argument. Whether you need to make it a formal induction proof depends on your instructor. – almagest Jun 17 '16 at 16:02
  • Unfortunately, I don't have an instructor or a TA to offer me any guidance. I am taking this course on my own accord off of MIT OCW. I want to stay true to the way the course notes teach induction proofs. So, I should start with a base case, $P(0)$. Then I need to establish my inductive step. I am unsure of how I should define those two steps. – Cherry_Developer Jun 17 '16 at 18:03
  • 1
    If you want to cast it as induction. Assume there are initially less than $n$ infected, so the boundary length at the start is $B_0<4n^2$. Your inductive hypothesis is $H_k$: after $k$ moves, the boundary is at most $B_0$. So it is trivially true for $k=0$. Suppose it is true after $k$ moves. You show it cannot increase. Hence it is true after $k+1$ moves. Hence by induction it is true after any number of moves. Now suppose that after $N$ moves the array is filled. Then boundary $=4n^2>B_0$. Contradiction. Hence it the array cannot be filled. – almagest Jun 17 '16 at 18:16
  • I apologize for taking so long to respond to your last comment. Something came up, and it took priority over self-studying. I used you advice along with other resources I found in order to formulate a proof for this using formal induction. I will type it up as an answer to this question. I would be very grateful if you could look it over. Thank you for your help. – Cherry_Developer Jun 25 '16 at 14:33
  • Sure. I will look out for it. – almagest Jun 25 '16 at 14:46
  • I have added it. – Cherry_Developer Jun 25 '16 at 14:57
  • Wrote some code to simulate the "beaver flu" process for arbitrarily large grids / initially infected students. Also highlights @almagest 's insight re: boundary lengths. (Hope it helps others who're attempting this problem!) – Per48edjes Jul 16 '22 at 19:53
2

Theorem: If fewer than $n$ students in class are initially infected, the whole class will never be completely infected.

Proof: by induction. We define perimeter of an infected set of students as the number of edges with infection on exactly one side. We let $x$ denote the size of the perimeter.

Let $P(k)$ be the proposition that after $k$ discrete time-steps, the perimeter is less than $4n$.

Base Case: $P(0)$ is true.

This is trivially true since the perimeter could not have possible changed after $0$ discrete time-steps. The perimeter of the infected region remains to be $x$.

Inductive Step: for all nonnegative integers, we must show that $P(k)\Rightarrow P(k+1)$

We assume that $P(k)$ is true for purposes of induction. So, this means that we are assuming that the perimeter of the infeted region is at most $x$ after $k$ steps.

At step $k + 1$, the perimeter of the infected region can only change in two ways. Since each newly infected square is adjacent to at least two previously infected squares, each newly infected square can either:

lose at least two edges from the perimeter of the infected region, or add at most two edges to the perimeter. Therefore, the perimeter of the infected region cannot increase.

So, we have shown that for all nonnegative integers, $k$, $P(k)\Rightarrow P(k+1)$

Q.E.D.

Cherry_Developer
  • 4,617
  • 1
    I think you want $P(k)$ to be the proposition that ... the perimeter is less than $4n$. Then $P(0)$ is true because the maximum perimeter would be 4 times the number of students (in the case when no students were adjacent). Your induction then goes through fine. But you need to add, that if the infection spread to the whole class after $N$ steps, then $P(N)$ would be false because the perimeter would be exactly $4n$ (the boundary round the array). Contradiction. So the infection cannot spread to the whole class. Then QED! – almagest Jun 25 '16 at 15:09
  • @almagest I'm sorry. I don't quite understand your reasoning for why $P(0)$ is true. From what I understand, it would be true because we have less than $n$ initially infected students to begin with. Thus, after 0 steps, the perimeter would still be less than $4n$. Is that correct? – Cherry_Developer Jun 25 '16 at 22:26
  • 2
    But $P(k)$ is the proposition that the perimeter is less than $4n$. So it is confusing to be told next that $P(0)$ is true because the perimeter remains $x$. What you want to establish is that $P(0)$ is true, ie that the perimeter is indeed less than $4n$. The reason for that is not that nothing has changed (that is obvious), but that $n$ infected individuals have a maximum perimeter of $4\times n$ (because each of the $n$ cells can contribute at most $4$ to the perimeter). Currently you do not state that anywhere. – almagest Jun 25 '16 at 22:35
  • @almagest So, would it be correct to say that $P(0)$ is true because we initially have less than $n$ infected students (according to the theorem), so the infected region cannot possibly have a perimeter of $4n$. So, the perimeter of the infected region is less than $4n$ after $0$ steps. Thank you for your help. – Cherry_Developer Jun 25 '16 at 23:12
  • 1
    I would stick to "because we initially have less than $n$ infected students, so the perimeter of the infected region must be less than $4n$". That is all you need, but you do need it. I don't like emphasis on 0 steps, that is just stating something that is obvious by definition. But it is not wrong. It is always a difficult judgment how much you need state to make things clear. – almagest Jun 26 '16 at 07:24
  • @Cherry_Developer are you considering adjacent squares as edges in the problem? Could you please elucidate how are you calculating the perimeter? – sarthak Jan 02 '17 at 20:55
  • 1
    @sarthak The perimeter of the infected region would be the combined perimeter of all the infected squares put together. – Cherry_Developer Jan 02 '17 at 23:02
0

Proof by Induction. Define the perimeter of an infected set of students to be the number of edges with infection on exactly one side. Let ν be size (number of edges) in the perimeter.

We claim that ν is a weakly decreasing variable. This follows because the perimeter changes after a transition only because some squares became newly infected. By the rules above, each newly infected square is adjacent to at least two previously-infected squares. Thus, for each newly infected square, at least two edges are removed from the perimeter of the infected region, and at most two edges are added to the perimeter. Therefore, the perimeter of the infected region cannot increase.

Now if an n × n grid is completely infected, then the perimeter of the infected region is 4n. Thus, the whole grid can become infected only if the perimeter is initially at least 4n. Since each square has perimeter 4, at least n squares must be infected initially for the whole grid to become infected.

Farruh Habibullaev
  • 101