My teacher said that in the circumference of circle there are infinite points. When I was learning more about circle, I came to this picture:
My question is: When we unroll the circle, then the length of the circle and line segment are the same. For this reason, I think that the unrolled line segment should also have infinite points! But there are only two end points. Can anyone explain to me where am I going wrong?
You are conflating end points and points.
Sidenote: The length of the segment is not as important as you may think. We cannot distinguish the number of points on a line segment of length $π$ from those on a line segment of length $2π$.
Both the circumference and the segment have infinitely many points, but that's not the point (heh, heh).
What matters is their length. The picture presumably is trying to show the ratio between the diameter and the circumference, which turns up to be $\pi$, or 3 and then something.
There are more than two points on a line segment. In fact, there are infinitely many points on the line segment. For example, there is a point between the two endpoints that is also in the line.
And a point between the middle point and the start.
And one between the middle and the end.
And one at a distance of $\frac{\pi^2}{4}$ from the start and on and on and on...
In the case of the circle, you take a polygon and say that it approximates a circle, but it is not precise. As you increase the number of points on the polygon, it approximates a circle more and more, but never quite reaches it. It is said that as the limit of points on the polygon approaches infinity, you have yourself a circle, which is why one interpretation of a circle is a polygon of infinite points.
In the second case, a line may have infinite points between its endpoints, however it is not a defining feature of the point. In other words, it doesn't become more "line"-like with increased points on the same line. However your assumption is not wrong! You could think of the line rolled out from a circle as having infinite points! Most people just tend to prefer to define a line in terms of its start and end points.
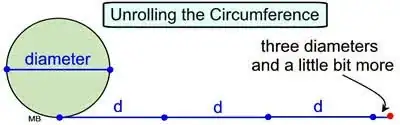
Another Pointless Discsussion! :-) On to a tangential question... It is all relative to the scale that is being examined. But points are dimensionless. So I take issue with the precise idea that a tangent can be determined by two points that are in close proximity. "Leibniz defined it as the line through a pair of infinitely close points on the curve." Wikipedia. The problem is, no matter how close two points are, there are an infinite number of points between two inifnitely close points. A better definition is to think in terms of tuples. A curve consists of an infinite set of tuples. For each tuple in that curved line, there only one tuple at a time can be concurrent with a tuple in an intersecting straight line. When that straight line intersects precisely that one point tuple in the curved line, then the straight line is a tangent. Now, practically (why differentian and integration was invented), there had to be a way to call "Close Enough" and converge to an answer. That works when the measurements needed to find that precise tuple, are below the level of accuracy possible for the scale you are working with.
So it matters that points are dimensionless and infinte in all mathematical applications. But to be practical, and make sense of a problem, points have to be defined in a way that is useful to the scale that the problem exists in. For example, if you zoom into a circle far enough, geometrically, the segment you are examining will appear to be a straight line, because the remaining curve falls below measurability. Practically, it becomes a straight line. Mathematically, the infinite set of tuples representing the curved line, is still curved.
Any legitimate question depends on whether the terminology is understood correctly. The problem is, the definition of a "point" is not understood correctly. Your teacher believes a point has no size because most, if not all, of the geometry books, old and new, say so. It is an error of immense proportions, wasting people's time and even warping their thinking. Geometry is supposed to help us understand the physical world around us. If a point has no size, then it has zero size. Basic math tells us that no matter how many times you add zero, it will always equal zero.
The correct definition of a POINT is "the smallest possible size". From there, everything will make sense mathematically, and logically. Both a circle, and a line segment, have an "indefinite" amount of points, but surely finite.
