11

I have a second order differential equation, \begin{eqnarray} \dfrac{d^2 y}{d x^2} = H\left(x\right) \hspace{0.05ex}y \label{*}\tag{*} \end{eqnarray}

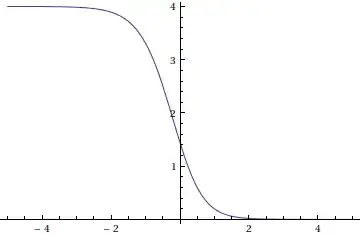
where, $\,H\left(x\right) = \dfrac{\mathop{\rm sech}\nolimits\left(x\right) \mathop{\rm sech}\nolimits\left(x\right)}{x + \ln\big(2\cosh\left(x\right)\big)}$. Plot of function $\,H\left(x\right) $ is shown below: enter image description here

I need to find solution of the equation $\eqref{*}$ for the boundary conditions

$$\begin{aligned} y\left(x\right)\bigg\rvert_{-\infty} &= 0, & \left.\dfrac{d\hspace{0.1ex}y\left(x\right)}{d\hspace{0.1ex}x}\right\rvert_{ -\infty} &= 0 \end{aligned} \label{**}\tag{**}$$

Obvious solution of the problem is $\,y=0$. But $\,y = x + \ln\big(2 \cosh\left(x\right)\big)\,$ also satisfies differential equation $\eqref{*}$, and satisfies boundary conditions $\eqref{**}$. Plot of $y\left(x\right)$ is shown below: enter image description here

As far as I know there cannot be two solution of the differential equation satisfying given boundary conditions. What am I missing here? Is uniqueness theorem not valid if the boundary conditions are applied at $\,\pm\infty$.

EDIT Thanks to the comment by Santiago, appearance contradiction is better seen:

Differential eq. $%\begin{align} y'\left(x\right) = y\left(x\right) %\end{align} $ with boundary condition $\displaystyle\lim_{x \to \infty}y\left(x\right) = 0$. There are infinitely many solution to this problem all of the form $y\left(x\right) = k\exp\left(x\right)$, where $k$ is some constant.

Post Edit Is it possible to generalize observation above that, boundary conditions at $\pm \infty$ may not yield unique solution?

Vlad
  • 6,938
alekhine
  • 399
  • 2
    Compare with $y'(x) = y(x)$ given that $y(-\infty) = y'(-\infty) = 0$. There are two solutions, $y \equiv 0$ and $y(x) = \exp x$. – Santiago May 03 '16 at 18:36
  • @Santiago, I see your point and completely agree with the example. – alekhine May 03 '16 at 18:53
  • @alekhine : This is the same for second order. Coming back to your example, with the simplest case $\quad H(x)=1\quad\to\quad y''(x)=y(x)\quad$ an infinity of solutions $\quad y=c,e^x\quad$ any $c$ , satisfy the two conditions $y(-\infty)=y'(-\infty)=0$ . – JJacquelin May 04 '16 at 08:32
  • Another exemple with finite boundary conditions : The EDO : $\quad x^2y''(x)=6y(x)\quad$ with two conditions $\quad y(0)=y'(0)=0\quad$ has an infinity of solutions : $\quad y(x)=c,x^3\quad$ – JJacquelin May 04 '16 at 08:56
  • 1
    Your last example is not surprising since $1/x^2$ is not locally lipschitz (not even $C^0$). The cauchy-lipschitz (or picard lindelöf) theorem guarantee the uniqueness and existence of solutions of $y'=f(x,y)$ if $f$ is locally lipschitz. But there is another theorem for which $f$ is only supposed continuous and then you have existence of a solution but not uniqueness. See "peano existence theorem". – Renart May 13 '16 at 12:24
  • Make some substutition to transform the interval into a finite one. Then check conditions of E&U for the transformed equation. – bkarpuz May 17 '17 at 12:17

1 Answers1

2

Consider the constant coefficient first order linear dynamical system of dimension $n$ \begin{equation}{\bf{x}}'=A{\bf{x}},\end{equation} where $A$ is an $n\times n$ constant matrix and ${\bf{x}}$ is an $n$-dimensional vector. If $A$ has $k$ eigenvalues with positive real parts, then system above has a $k$ dimensional space of solutions satisfying $\displaystyle{\lim_{t\rightarrow-\infty}{\bf{x}}=0}$.

More generally, we now consider a class of equations which the system (*) in the question is part of. More precisely, we consider systems of the form \begin{equation}{\bf{x}}'=A(t){\bf{x}},\end{equation} where $A$ is $t$-dependent and such that the limit $A^{-\infty}\equiv \displaystyle{\lim_{t\rightarrow -\infty} A(t)}$ exists. Assume also that $A(t)$ approaches $A^{-\infty}$ exponentially fast as $t\rightarrow -\infty$. Then the solutions of the system above behave like the solutions of the constant coefficient system $$ {\bf{x}}'=A^{-\infty}{\bf{x}}, $$ as $t\rightarrow -\infty$, which in particular implies that If $A^{-\infty}$ has $k$ eigenvalues with positive real parts, then the non-constant system above has a $k$ dimensional space of solutions satisfying $\displaystyle{\lim_{t\rightarrow -\infty}{\bf{x}}=0}$.

Gateau au fromage
  • 1,282