20
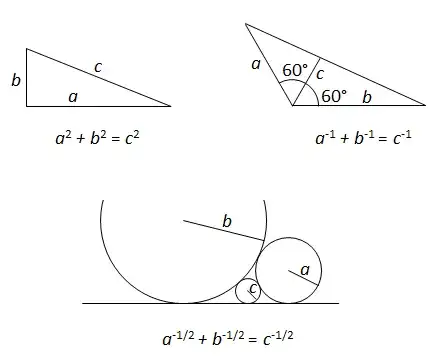
  • The Pythagorean theorem.
  • Let $A$, $C$, $B$ be three points on a line in this order, and let $D$ be another point, such that $\angle ADC =\angle CDB = 60^\circ$. Let $a=AD$, $b=BD$, $c=CD$. Then, $$a^{-1} + b^{-1} = c^{-1}.$$
  • Let $C_1$, $C_2$, $C_3$ be three circles that are tangent to each other and also tangent to a common line, such that $C_3$ lies between $C_1$ and $C_2$. Let $a$, $b$, $c$ be their respective radii. Then, $$a^{-1/2} + b^{-1/2} = c^{-1/2}.$$

See the figure below.

Are there any other results of this type in geometry?

enter image description here

ACB
  • 3,948
Gabriel Nivasch
  • 909
  • 2
    laughs internally – Edward Evans Mar 31 '16 at 18:02
  • where are the points $$A,B,C,D$$? – Dr. Sonnhard Graubner Mar 31 '16 at 18:03
  • $D$ is the vertex of the two 60-degree angles. $A$, $B$, and $C$ are the other endpoints of the segments $a$, $b$, $c$, respectively. – Gabriel Nivasch Mar 31 '16 at 18:06
  • 4
    A rather trivial one: if $A,B,C$ lie on a line in this order and $AB=a,BC=b,CA=c$, then $a^1+b^1=c^1$. – Wojowu Mar 31 '16 at 18:09
  • 2
    :) I was waiting for someone to say that... – Gabriel Nivasch Mar 31 '16 at 18:09
  • I honestly would expect some nice relation with $x=1/2,-2$ beyond the ones mentioned, and I will be really surprised to see ones with more "exotic" exponents. Just a gut feeling though. – Wojowu Mar 31 '16 at 18:13
  • See: this – Edward Evans Mar 31 '16 at 18:36
  • 3
    That's not exactly related. I'm not requiring a,b,c to be integers, and I want a^x+b^x=c^x to be a theorem related to some (geometrical) construction. – Gabriel Nivasch Mar 31 '16 at 18:38
  • Also we have Pythagorean theorem for reciprocals, but usually we use $h$ instead of $c$ there. :) – ACB Dec 11 '21 at 12:05
  • We have some relations with $x=-1$, as mentioned in my previous comment, they have $a$ and $b$ but not $c$ :D. So I don't think they'll fit here. (IMO, it's a surprize to see that there are only three answers in this big list.) – ACB Dec 11 '21 at 12:23
  • That one is already mentiond by zyx @Flagged – nonuser Dec 11 '21 at 12:39
  • @Aqua , yes, now I see zyx saying "There must be many more". He/she has condensed all answers to his/her post. :) P.S. : If you are talking about my second comment, I was thinking about some other incidents, including quadrilaterals inside a triangle etc. I'll leave it here as a hint for someone else to find out. ; ) – ACB Dec 11 '21 at 13:41

3 Answers3

10

Here's another one. Let $ABCD$ be a trapezoid of area $c$ and let $O$ be the intersection point of its diagonals. If $a$ and $b$ are areas of triangles $AOD$ and $BOC$ (or $AOB$ and $COD$) then $$a^{1/2}+b^{1/2}=c^{1/2}.$$

enter image description here

CuriousGuest
  • 4,341
8

Exponents $1,2, -1, -2,1/2$, and $-1/2$ are probably the most common, with the complexity of the implied polynomial equation $P(a,b,c)=0$ increasing in that order. As a random example, the height in the crossed ladders problem satisfies $h^{-1} = a^{-1} + b^{-1}$. For the altitude of a right triangle, $h^{-2} = a^{-2} + b^{-2}$. There must be many more.

Exponent $2/3$: the envelope of a line segment of length $L$ with endpoints on the $x$ and $y$ axes is $x^{2/3} + y^{2/3} = L^{2/3}$. The curve is called astroid.

zyx
  • 36,077
  • Nice. Whenever you recall any other examples, put them in. – Gabriel Nivasch Apr 03 '16 at 14:13
  • 1
    The last example generalizes somewhat: the envelope of lines whose x and y intercepts satisfy $a^u + b^u = L^u$ is the curve $x^p+y^p=L^p$ for $p$ Hoelder dual to $-u$. Another geometrically meaningful case is when $a+b=L$ so that the dual is $\sqrt{x}+\sqrt{y}=\sqrt{L}$. – zyx Apr 04 '16 at 00:14
4

Here's another one. I don't think it's much popular, but the proof is not too terrible.

image

$$\large a^{2/3}+b^{2/3}=c^{2/3}$$

ACB
  • 3,948