2

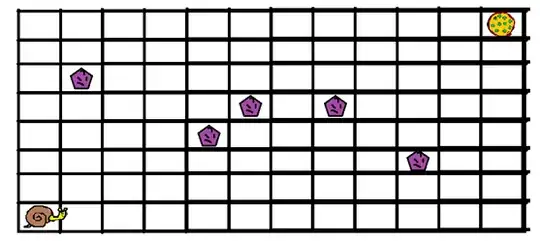
enter image description here

Calculate the number of ways of getting to the pizza without stepping on bombs (you can move up and right)

My solution was to calculate the number of ways of getting from the snail to the pizza (without the including the bombs) and subtracting from that number the number of ways of getting from any bomb to the pizza. Thereafter, adding to it the number of ways where you step on two bombs and get to the pizza. Finally, I add to that number the number of ways of stepping on three bombs and getting to the pizza. (All from the Inclusion–exclusion principle). My final answer was: $$31293$$ Am I correct? Can you spot any mistakes I've made along the way? Thank you!

(Edit: I counted those ways by looking at the permutations of choosing a certain number of steps to the right, $x$ from the sum of steps to left and right $x+y$, so: $$\binom{x+y}{x}=\binom{x+y}{y}$$ See: How can I find the number of the shortest paths between two points on a 2D lattice grid?)

Community
  • 1
Mike B.
  • 120
  • 1
    How did you calculate the number of ways? Showing that will be helpfull. – MathematicianByMistake Mar 20 '16 at 21:13
  • That seems to be sound. Watch out for double counting but you seem to have thought about that. – fleablood Mar 20 '16 at 22:03
  • "and subtracting from that number the number of ways of getting from any bomb to the pizza" Shouldn't that be number of ways for bomb to pizza multiplied by number of ways from snail to bomb? ... if there are 6 ways to get from the snail to the bomb and 7 ways to get from the bomb to the pizza, then there are 42 ways to get from the snail to the pizza by going through the bomb. – fleablood Mar 20 '16 at 22:07
  • I'm on it thank you very much – Mike B. Mar 20 '16 at 22:08

1 Answers1

1

Simple counting seems less tedious than using the inclusion-exclusion principle:

answer

Every rectangle has a number which denotes the number of ways to reach to that rectangle from the lower-left corner. To reach that number, just add the values of left and down rectangles. Obviously, putting $0$ in place of the bombs before calculations is fitting with that general rule.

Alistair
  • 1,770