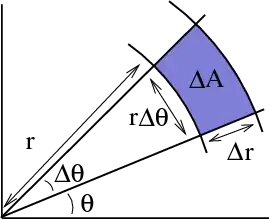
Given is $d^3x = dxdydz$ and I need to convert it to cylindrical coordinates (given through: $x = r\cos\varphi$ and $y = r\sin\varphi$).
The expected result is: $(dz)(dr)(r)(d\varphi)$ and I cannot seem to get it right.
This is what I am doing:
$dz = dz$
$dy = \frac{dy}{d\varphi} d\varphi = r \cos\varphi d\varphi = \frac{dy}{dr} = \sin\varphi dr$
$dx = \frac{dx}{d\varphi} d\varphi = - r \sin\varphi d\varphi = \frac{dx}{dr} dr = \cos\varphi dr$
But I can't see how to create the expected solution from this.