11

Let G be a grid graph with m rows and n columns, i.e. m = 4, n = 7 is shown here:

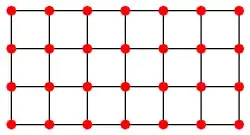
grid graph with 4 rows, 7 columns

For what values of m and n does G have a Hamilton path, and for what values of m and n does G have a Hamilton cycle?

So far I've figured out that a grid graph always has a Hamilton path, and has a Hamilton cycle when at least one of m or n is even. I'm struggling to provide justification as to why this is true...

Jim Jj
  • 187

3 Answers3

9

This is a more formal construction, building off of the answers by Brian M. Scott and David Ongaro.

The theorem is actually: an n x m grid graph is Hamiltonian if and only if:

A) m or n is even and m > 1 and n > 1

or

B) mn = 1

There are four parts to the proof.

Part 1: If either m or n is even, and both m > 1 and n > 1, the graph is Hamiltonian

This proof is going to be by construction.

If one of the even sides is of length 2, you can form a ring that reaches all vertices, so the graph is Hamiltonian.

Otherwise, there exists an even side of length greater than 2. Let's call that direction "vertical" and the other direction "horizontal". Thus, the graph has an even number of rows. Take one of the vertical edges of the graph and make a starting path connecting all squares on that edge. Then, the ends of the starting path can be extended through the rest of the nodes by creating "switchbacks", paths that run out to the edge of the grid opposite the starting path using one horizontal row of squares and then back to the column adjacent to the starting path using the next horizontal row. A complete switchback will reach all of the nodes in its rows that aren't reached by the starting path and requires 2 rows. Since there are an even number of rows in the graph, we can fill the remainder of the graph with switchbacks and end in a square adjacent to the open end of the starting path. Connecting the final switchback to the open end of the starting path creates a Hamiltonian cycle.

Ex:

* - * - * - * - *
|               |
*   * - * - * - *
|   |
*   * - * - * - *
|               |
*   * - * - * - *
|   |
*   * - * - * - *
|               |
* - * - * - * - *

Part 2: If mn = 1, the graph is Hamiltonian

If both mn = 1, then it is a 1 vertex graph. This is trivially Hamiltonian in that there is a zero length path that visits the vertex. [1]

Part 3: If m = 1 xor n = 1, the graph is not Hamiltonian

All Hamiltonian graphs are biconnected. [2]

If exactly one of the dimensions is 1, then the graph is a line of length at least 2. If the length is 2, then it is a simple graph with 2 vertices. There are no simple 2-node Hamiltonian graphs (OEIS A003216), so this is not Hamiltonian.

If the length is greater than 2, there must be a central vertex of the graph that can be removed and the graph will become disconnected. Thus, the graph is not biconnected and is therefore not Hamiltonian.

Part 4: If both m and n are odd and mn != 1, the graph is not Hamiltonian

Any bipartite graph with unbalanced vertex parity is not Hamiltonian. [3][4]

You can color the grid like a chess board, such that alternating squares are black and white and no two adjacent squares share a color. Noting that squares of the grid are vertices of the graph, it follows that the set of black vertices and the set of white vertices are a partition of the graph into 2 sets such that none of the vertices in the same set are adjacent. Thus, the graph is bipartite. Since both of the dimensions are odd, the total number of squares and therefore vertices is odd, so therefore the partitions must have different numbers of vertices. As a result, the graph is bipartite with unbalanced vertices and isn't Hamiltonian.

Zags
  • 267
4

HINT: You simply need to explain carefully how to produce the desired paths.

  • There is always a Hamilton path that simply traverses the rows in alternate directions.

  • If, say, $m$ is even, as in your example, you can generalize the following idea (which I’ve left slightly incomplete). The evenness of $m$ is what makes the idea work.

      *-->*-->*-->*-->*  
                  | 
                  V  
  *   *<--*<--*<--*  
      |  
      V  
  *   *-->*-->*-->*  
                  |  
                  V  
  *<--*<--*<--*<--*
Brian M. Scott
  • 631,399
3

To prove why it works when $mn$ is even and $m, n > 1$ it should be enough to provide a construction of a Hamiltonian cycle as Brain did in his answer.

To prove why there is no such cycle when $mn$ is odd consider the following: color each vertex as "black" when the sum of its coordinates is even otherwise as "white". In this way you get a checkerboard pattern and no likewise colored vertexes are connected. Since the total number of vertexes is odd the start and endpoints of a Hamiltonian path must have the same colors, therefore they can not be connected.

David Ongaro
  • 251