Create a formula that creates a curve between two points

Question

We have two points, $A$ and $B$. The difference in $x$ is 1 unit, and the difference in $y$ is arbitrary. For each point we also know the gradient. First, I want to draw a smooth line that connects both points and smoothly transitions between gradients. Then, I want a function that returns a $y$-value for any value of $x$ between $A$ and $B$, where $0 < x < 1$.

What do you mean by "smoothly transition" between gradients. There is lots of ways to do this and your definition of "smoothly" will affect what method you use. — Ian Miller, Mar 13 '16 at 07:20
by gradient I mean rise/run of the tangent at that point. By "smoothly transition" I mean that the gradient changes in as a function of x. — Lorry Laurence mcLarry, Mar 13 '16 at 07:31
So you want $f'(x)$ continuous at the change. Do you also want other derivatives continuous at the change (for" smoothness")? — Ian Miller, Mar 13 '16 at 07:43
I think Adriano has more or less nailed it. He wrongly assumes that f(0)=0, but I was able to work around that by adding and subtracting 'ya'. — Lorry Laurence mcLarry, Mar 13 '16 at 10:33

score 1 · Answer 1 · answered Mar 13 '16 at 07:19

You have 4 conditions: $f(x_a)=y_a$, $f(x_b)=y_b$, $f'(x_a)=m_a$ and $f'(x_b)=m_b$. As such you need a cubic equation - $f(x)=ax^3+bx^2+cx+d$.

This is known as a cubic spline. There are other types of splines which may be more suitable for your application but will involve harder mathematics.

You should be able to find lots with a simple google search.

score 1 · Accepted Answer · answered Mar 13 '16 at 07:20

1

Assume that our conditions are: $$ f(0) = 0,~~ f(1) = b,~~ f'(0) = p,~~ f'(1) = q $$ and that we use a cubic polynomial $f(x) = a_3x^3 + a_2x^2 + a_1x + a_0$. Solving this system of equations yields: $$ f(x) = (p + q - 2b)x^3 + (3b - 2p - q)x^2 + px $$

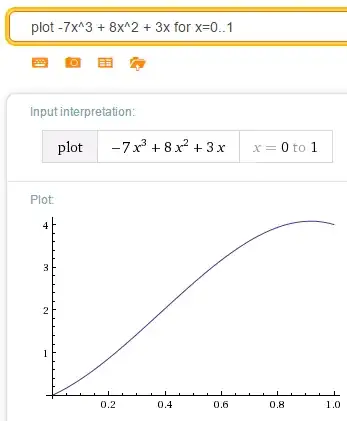
For example, if our first point is $(0, 0)$ with a gradient of $p = 3$ and our second point is $(1, 4)$ with a gradient of $q = -2$, then our curve is: $$ f(x) = -7x^3 + 8x^2 + 3x $$ Indeed, the plot looks like:

answered Mar 13 '16 at 07:20

Adriano

41,969

what plotting software are you using to produce the images in your answer? – Reinsbrain Jul 15 '19 at 13:57
Wolfram|Alpha: https://www.wolframalpha.com/input/?i=plot+-7x%5E3+%2B+8x%5E2+%2B+3x+for+x+%3D+0..1 – Adriano Jul 15 '19 at 17:46

score 0 · Answer 3 · edited Jun 12 '20 at 10:38

The curve

$$f(x) = (p + q - 2b) (x / k) ^ 3 + (3b - 2p - q) (x / k) ^2 + p (x / k) + m$$

The first point is (0 , m) and the second is (k , (m + b))

First and second point:

$$f(0) = m$$ $$and$$ $$f(k) = m + b$$

The gradient of the first and second point:

$$f'(0) = p / k$$ $$and$$ $$f'(k) = q / k$$

The y value in the middel:

$$f(k / 2) = (p - q + 4 (b + m)) / 4$$

The tangent in the middel:

$$f(k / 2) = 3xb / 2k - x (p + q) / 4k + (p - b + 4m) / 4$$