5

i am currently pursuing a course in basic homology theory.i am really stuck in how to triangulate a torus by using simplicial complexes . in every book, a diagram is given but it does not define that why are we subdividing the sheet into a no of rectangles etc,i.e,ther is no explanation given .I know that this is a very basic question but i cannot find a solution on the internet.

if possible,please give an explanation.also,mention references for solved examples on triangulation of a space using simplicial complexes and cw complexes...

thanks a lot

Michael Hardy
  • 1
Abhishek Shrivastava
  • 880
  • 10
  • 19

1 Answers1

11

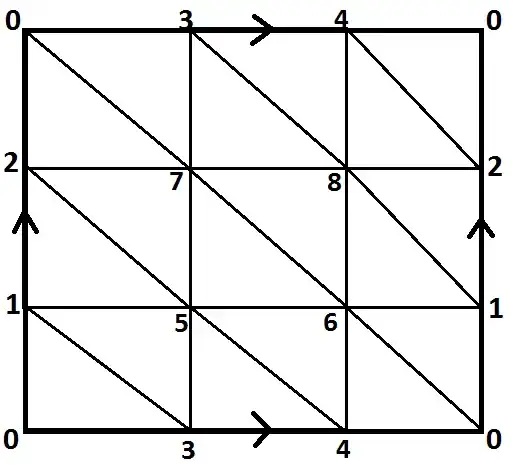
Triangulation of the Torus

Sorry for the bad quality of the picture. It shows a possible triangulation of the Torus.

Whenever you try to find a triangulation (in particular a Euklidian simplicial complex), it's a collection $K$ of simplicies satisfying the following conditions:

1.) $\sigma\in K$ $\Rightarrow$ every face of $\sigma$ is in $K$.

2.) The intersection of any two simplicies is either empty or a face of both.

3.) For every point in $\sigma\in K$ there exists a neighbourhood which intersects finitely many simplices of $K$.

Let $\{v_0,...,v_n\}$ be the vertices of $\sigma \in K$. A face of $\sigma$ is the simplex spanned by each non-empty subset of $\{v_0,...,v_n\}$.

The most important point is: If you try to triangulate a surface, any two triangles share a single edge or a single vertex or they're disjoint.

A non-example:

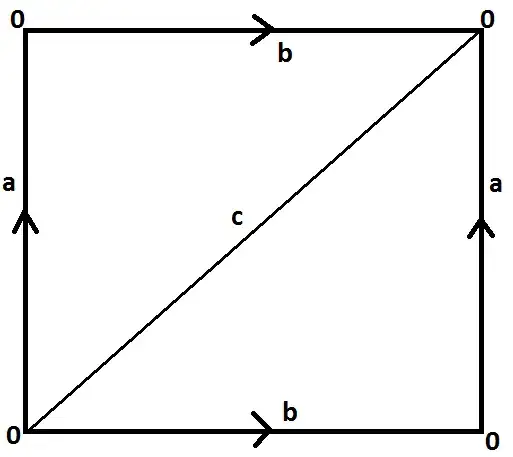
False

This triangulation is false, because the two "triangles" are no triangles. They share 3 edges and the vertices are identified (more on: Triangulation of Torus).

If you would like to calculate the homology goup by using a CW complex, you just take a 0-cell and attach two 1-cells. Then you attach one 2-cell. The following video gives you an impression how to glue the 2-cell, although this video is not originally made for illustrating this: https://www.youtube.com/watch?v=nLcr-DWVEto

To get an intuitive understanding of the subject, I recommend you to watch the videos of Wildberger: https://www.youtube.com/watch?v=Uq4dTjHfLpI

Community
  • 1
Daniel Bernoulli
  • 1,938
  • but in wildberger videos i was not able to find examples on using simplicial complexes ,rather he used cw complexes for triangulations... – Abhishek Shrivastava Feb 17 '16 at 15:45
  • 1
    Sorry, my mind played a hoax on me. ;-) But you can find a lot of calculations on this site, e.g. http://math.stackexchange.com/questions/1184275/simplicial-homology-of-sphere-with-bars. Ex.: Calculation of the disc $\cong$ filled triangle with verticies ${0,1,2}$. $\mathbb{Z}[0,1,2]\overset{\delta_2}{\to} \mathbb{Z}[0,1]\oplus\mathbb{Z}[0,2]\oplus\mathbb{Z}[1,2]\overset{\delta_1}{\to}\mathbb{Z}[0]\oplus\mathbb{Z}[1]\oplus\mathbb{Z}[2]$ is the exact sequence of the complexes. Just kill permutations and repititions. $\delta_1:[0,1]\mapsto[1]-[0]$ and so on. Compute Ker and Im of $\delta_i$. – Daniel Bernoulli Feb 18 '16 at 07:23
  • 1
    Permutations and repetitions get killed in the term of $\bigoplus_{v=(v_0,...,v_q)...}\mathbb{Z}v$. Consider $H_i(C_\cdot )=Ker(\delta_i)/Im(\delta_{i+1})$. To understand the example better I recommend you to read https://en.wikipedia.org/wiki/Simplicial_homology. – Daniel Bernoulli Feb 18 '16 at 07:29