3

I am looking for iterative procedures for solution of the linear least squares problems with linear equality constraints.

The Problem:

$$ \arg \min_{x} \frac{1}{2} \left\| A x - b \right\|_{2}^{2}, \quad \text{subject to} \quad B x = d $$

How can best the two systems can be combined so that iterative procedures can be applied on it?

Royi
  • 10,050
Salman Zeb
  • 31
  • 3

4 Answers4

3

The easiest and most straight forward iterative method would be the Projected Gradient Descent.

Projection onto Linear Equality Equation

The Projected Gradient Descent requires a projection step onto the Linear Equation constraint.
The problem is given by:

$$ \arg \min_{x} \frac{1}{2} \left\| x - y \right\|_{2}^{2}, \quad \text{subject to} \quad B x = d $$

From the KKT Conditions one could see the result is given by:

$$ \hat{x} = y - {B}^{T} \left( B {B}^{T} \right)^{-1} \left( B y - d \right) $$

Full derivation is given at Projection of $ z $ onto the Affine Set $ \left\{ x \mid A x = b \right\} $.

Now, all needed is to integrate that into the Projected Gradient Descent framework.

%% Solution by Projected Gradient Descent

hObjFun     = @(vX) (0.5 * sum((mA * vX - vB) .^ 2));
hProjFun    = @(vY) vY - (mB.' * ((mB * mB.') \ (mB * vY - vD)));
vObjVal = zeros([numIterations, 1]);


mAA = mA.' * mA;
vAb = mA.' * vB;


vX          = mB \ vD; %<! Initialization by the Least Squares Solution of the Constraint
vX          = hProjFun(vX);
vObjVal(1)  = hObjFun(vX);


for ii = 2:numIterations


vX = vX - (stepSize * ((mAA * vX) - vAb));
vX = hProjFun(vX);

vObjVal(ii) = hObjFun(vX);



end

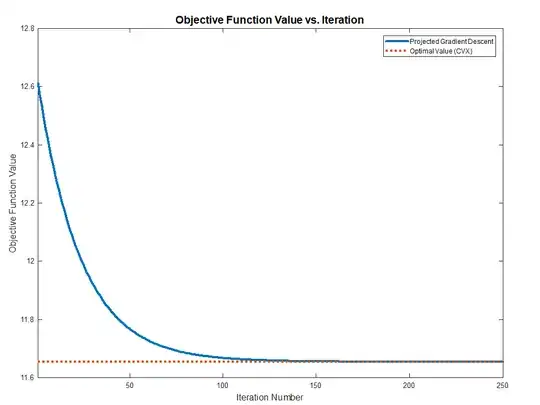
enter image description here

The full code, including validation using CVX, can be found in my StackExchange Mathematics Q1596362 GitHub Repository.

Royi
  • 10,050
0

Let $A\in M_{m,n}$ with $rank(A)=n\leq m$, that is, $A$ is one to one. Let $B\in M_{k,n}$ with $0<r=dim(\ker(B))<m$; here $x\in \mathbb{R}^n,d\in\mathbb{R}^k$. Thus $x\in \Pi$, an affine subspace of dimension $r$ of $\mathbb{R}^n$ and $Ax\in A(\Pi)$, an affine subspace of $\mathbb{R}^m$ of dimension $r$. If $x_0$ is the required solution, then $Ax_0$ is the orthogonal projection of $b$ on $A(\Pi)$.

Method 1. We seek a basis $(e_1,\cdots,e_r)$ of $\ker(B)$; then $(Ae_1,\cdots,Ae_r)$ is a basis of $A(\ker(B))$; we deduce an orthonormal basis (by Schmidt process) of $A(ker(B))$ ....

Method 2. Use the Lagrange method. The unknowns are $x\in \mathbb{R}^n$ and $\Lambda\in M_{1,k}$ and the $n+k$ linear equations are $Bx=d,2(Ax-b)^TA+\Lambda B=0$.

0

A quick and dirty way that I have seen work well in practice is to minimize $$||Ax-b||+\lambda||Bx-d||$$ using iterative methods such as Levenberg-Marquardt. In your case, I would set a higher value for $\lambda$. In case finding a correct $\lambda$ is difficult (because of scale differences, etc), you can minimize $$\frac{1}{s-||Bx-d||}+||Ax-b||$$ where s is a threshold that you do not want ||Bx-d|| to exceed (in that case, you might want to initialize your minimization algorithm with the $x$ that minimizes $||Bx-d||$).

Ash
  • 689
  • 1
  • 7
  • 19
  • a quick and non dirtay way is to notice that when $\lambda \to \infty$ minimizing $||Ax-b||^2+\lambda||Bx-d||^2$ is equivalent to minimize $||A ( B^+ d + B^{\perp} y) - b||^2$ and setting $x^* = ( B^+ d + B^{\perp} y^*)$ yields the desired solution – reuns Jan 21 '16 at 10:12
  • This is not obvious to me... Could you please explain (or post an answer, I'll be the first to upvote)? – Ash Jan 21 '16 at 18:02
  • when $\lambda \to \infty$ : $Bx^* \to d$ – reuns Jan 21 '16 at 19:08
0

I would propose reweighted linear least squares.

This way you can get away with only a simple least squares solver and very little overhead in updating the weight matrix.

$$+w\|Bx-d\|_2^2$$

Where the weight $w$ is updated to enforce the equality more and more in between iterations. You can even try a very big $w$ at the start. Maybe you don't even need much of reweighting.

mathreadler
  • 26,534