OK, your outer solution is, at leading order,
$$y_0=x^2+C, $$
and matching the left hand boundary condition gives $C=1$, and matching the right hand boundary condition gives $C=3$. So there must be a boundary layer somewhere in order to be able to satisfy both boundary conditions.
Let $x=x_0+\epsilon^\alpha X$, where $x_0$ is the location of the layer (so $-1\leq x_0\leq2$) and $\alpha$ is yet to be determined, but is a positive number. Substituting into the differential equation and expanding gives
$$ 2\epsilon y+\epsilon^{1-2\alpha}y''+2\epsilon^{-\alpha}x_0y'+2Xy'-4x_0^2-8\epsilon^\alpha x_0X-4\epsilon^{2\alpha}X^2=0. $$
There are two cases to consider, if $x_0=0$ or $x_0\neq0$. First, consider $x_0\neq0$. Dominant balance on the scaled equation gives $\alpha=1$, and the leading order equation is
$$ y''-2x_0y'=0 $$
with solution
$$ y=A\exp(-2x_0X)+B. $$
Immediately, because the solution is exponential, we notice that the layer cannot be internal (except maybe at $x_0=0$, which are not considering here), because it will grow exponentially going out of the layer in one direction. Remember that we need the limit as $X$ goes out of the boundary layer to exist. If the layer is at $x_0>0$, the limit as $X\rightarrow-\infty$ does not exist, and if $x_0$ is negative, the limit as $X\rightarrow\infty$ does not exist. So the layer can't be anywhere except 0.
So $x_0=0$, but this changes the original scaled equation! We now have
$$ 2\epsilon y+\epsilon^{1-2\alpha}y''+2Xy'-4\epsilon^{2\alpha}X^2=0, $$
and dominant balance gives $1-2\alpha=0$, or $\alpha=1/2$. The leading order equation is
$$y''+2Xy'=0, $$
which has solution
$$ y=A\mathrm{erf}(X)+B. $$
Now, we have two outer soluions to match to, $x^2+1$ as $X\rightarrow-\infty$, and $x^2+3$ as $x\rightarrow\infty$. The matching conditions are, to the left,
$$ \lim_{X\rightarrow-\infty}A\mathrm{erf}(X)+B=\lim_{x\rightarrow0}x^2+1 $$
which gives $-A+B=1$, and to the right,
$$ \lim_{X\rightarrow\infty}A\mathrm{erf}(X)+B=\lim_{x\rightarrow0}x^2+3 $$
which gives $A+B=3$.
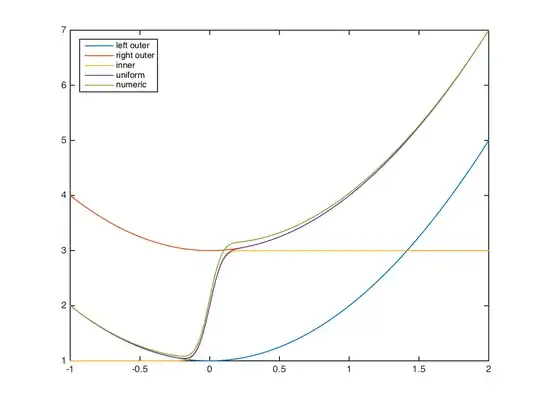
Solving these gives $A=1$ and $B=2$. The error function is effectively a jump of height 2, which moves the solution from one parabola to another.
You can make a uniform approximation, using either outer solution,
$$y_{unif}(x)=y_{outer}(x)-y_{outer}(0)+y_{inner}(x/\sqrt\epsilon)=x^2+\mathrm{erf}\left(\frac{x}{\sqrt\epsilon}\right)+2.$$
Of course we want to look at a picture too. The numerical solution wasn't easy to get, I usually use a simple shooting method and an ODE solver, but for this I had to use a BVP solver. In this picture, $\epsilon=0.01$ (boundary layer $\sim0.1$ wide)
I also used symbolic algebra to calculate the residual when you substitute $y_{unif}$ into the original differential equation. The result was
$$ 2\epsilon\left(\mathrm{erf}\left(\frac{x}{\sqrt\epsilon}\right) + x^2 + 3\right) $$ which is indeed $O(\epsilon)$ in $[-1,2]$, so everything looks alright.
