Plotting $\left(1+\frac{1}{x^n}\right)^{x^n}$.

Question

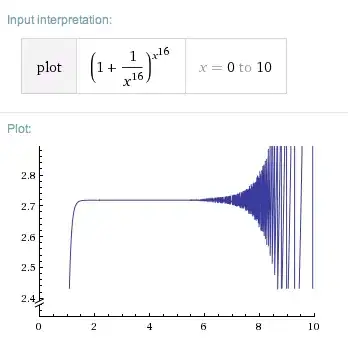
When I plot the following function, the graph behaves strangely:

$$f(x) = \left(1+\frac{1}{x^{16}}\right)^{x^{16}}$$

While $\lim_{x\to +\infty} f(x) = e$ the graph starts to fade at $x \approx 6$. What's going on here? (plotted on my trusty old 32 bit PC.)

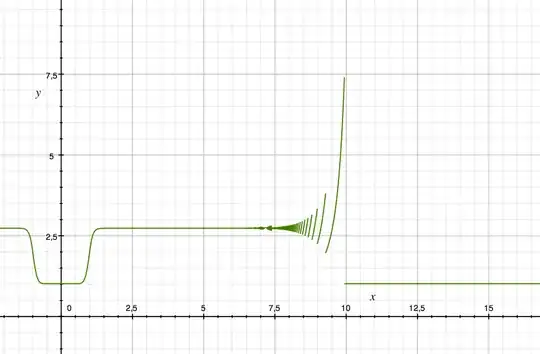
I guess it's because of computer approximation and loss of significant digits. So I started calculating the binary representation to see if this is the case. However in my calculations values of $x=8$ should still behave nicely.

If computer approximation would be the problem, then plotting this function on a 64 bit pc should evade the problem (a bit). I tried the Wolfram Alpha servers:

The problem remains for the same values of $x$.

Questions

1. Could someone pinpoint the problem? What about the 32 vs 64 bit plot?
2. Is there a way to predict at which $x$-value the graph of the function below would start to fail? $$f_n(x) = \left(1+\frac{1}{x^n}\right)^{x^n}$$

Answer 1

32bit vs. 64bit affects which integer types are used by default, which is of no interest here. Rather, the floting point computations are made (by default) with IEEE double type. With this double precision (53 bit mantissa), the relative error of $(1+\frac1{x^{16}})$ is approximately $2^{-53}$. Raising to the $x^{16}$th power roughly multiplies the relative error, so it's $\frac{8^{16}}{2^{53}}=2^{-5}$ (so absolutely $\approx 0.1$) for $x=8$, which does match your plot. At $x=9$ we can expect a relative error $\frac{9^{16}}{2^{53}}\approx0.2$, also consistent with your plot. For $x>10$ we have $x^{16}>2^{53}$, so $(1+\frac1{x^{16}})\dot=1$, whereas righ tbefore this cutoff to a terminally too small $(1+\frac1{x^{16}})$, we have a longer phase of too big in the last and only bit, i.e., we essentially compute $(1+\frac2{x^{16}})^{x^{16}}\approx e^2\approx 7.4$.

Answer 2

Your problem is the finite precision of floating-point arithmetic. There are only so many numbers near $1$ that can be represented by the computer's floating-point format, and the larger your $x$ is, the more of the difference between $1$ and $1+\frac{1}{x^{16}}$ (which is what really matters when raising to a huge power) will be lost to rounding of the latter intermediate result.

In order to make precise calculations with such expressions possible, many programming languages provide primitive functions for computing $x\mapsto \log(1+x)$ and $x\mapsto e^x-1$ directly, without ever representing the intermediate result $1+x$ and $e^x$ explicitly.

To use this in your case you would rewrite $$ (1+a)^b = e^{b \log (1+a)}$$ and write something like (e.g., in C, with <math.h>):

double x16 = pow(x,16);
double result = exp(log1p(1/x16) * x16);

---

You shouldn't expect any difference between computing on a 32-bit or a 64-bit machine, because even on "32-bit" machines the usual precision of floating point calculations is a 64-bit representation with about 16 significant digits of precision.

(Conversely, both 32-bit and 64-bit machines do support a 32-bit floating-point format, but operations on it are rarely any faster (in contrast to integer arithmetic, where 64-bit operations are slower on 32-bit machines), so in practice it is only used when one needs to store so many floating-point numbers that the combined size of them all becomes a concern.)

Answer 3

Here is a plot using the (arbitrary precision) calculator Pari/GP. I use 200 dec digits precision as default in my computations and got this plot without oscillation up to x=20:

I tried it so far up to x=256; no oscillation. See here the image up to x=128 (just to have the left increase visible)