It's pretty obvious to me as I see the plot of the two functions but how can I prove it with some algebra?
Asked
Active
Viewed 71 times
2
-
That does not seem true. Did you mean: $|\sin(x)|\leq|x|$? – Element118 Nov 05 '15 at 05:55
-
yeah, I'm sorry, thanks for the correction – Zauberkerl Nov 05 '15 at 05:55
-
What tools do you have available? Do you know, for example that $\sin x\le x$ for $x\ge 0$? – Mark Viola Nov 05 '15 at 05:59
-
The Lagrange Form of the Taylor Remainder Theorem? Link: https://en.wikipedia.org/wiki/Taylor%27s_theorem#Explicit_formulae_for_the_remainder – Christopher Carl Heckman Nov 05 '15 at 06:02
-
1The inequality comes from any arc between two point is longer than the straight line between the same points. Draw the triangle and the circle out and you will see it. – cr001 Nov 05 '15 at 06:04
4 Answers
2
By mean-value theorem, if $-1 \leq x < 0$, then $$ |\sin x - \sin 0| = |\sin x| \leq |x|\sup_{0 < t < x}|\cos t| \leq |x|. $$
Yes
- 20,910
2
So here's an answer involving Calculus:
consider $f(x)=x-\sin x $
$f'(x) =1- \cos x > 0$
for $x \in [0,1]$, $f$ is increasing, so $f(x)>f(0)=0$ for $x \in [0,1]$
which means $x>\sin x \implies |x|>|\sin x|$ since $x$ and $\sin x$ is positive here.
for $x \in [-1,0]$, $f$ is increasing, so $f(x)<f(0)=0$ for $x \in [-1,0]$
which means $x<\sin x \implies |x|>|\sin x|$ since $x$ and $\sin x$ is negative here.
Therefore $|x|>|\sin x|$ for $x \in [-1,1]$
More water plz
- 1,511
2
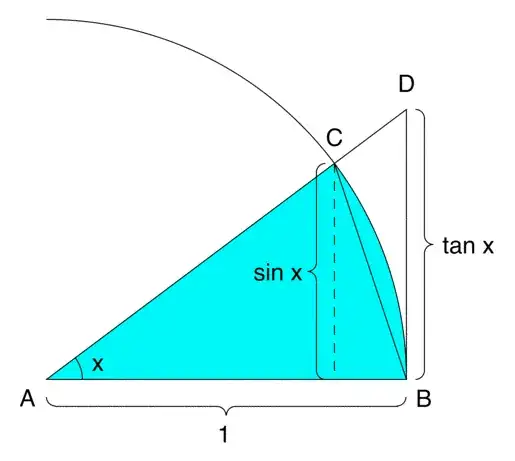
(image taken from robjohn's answer here)
A geometrical proof can be seen in the following image:
$\sin x$ is the height from $C$ which is smaller than $BC$, which, in turn is smaller than the length of the arc $BC$, which is equal to $x$.
Beni Bogosel
- 23,891
1
Use the mean value theorem:
There is some number $c$ between $x$ and $0$ for which $$ \sin' c = \frac{\sin x - \sin 0}{x - 0}. $$ Since $|\sin'c|=|\cos c|\le 1$, we have $$ \left|\frac{\sin x} x \right| \le 1, $$ so $$ |\sin x| \le |x|. $$ There is no need to assume $x$ is in $[-1,0]$ to get this conclusion.