What's so special about the 4 fundamental subspaces?

Question

I was reading Gilbert Strang's book for Linear Algebra (along with his lectures) and I feel that he is emphasizing that the 4 fundamental subspaces (Column Space, Row Space, Null Space and Null Space of $A^T$) form the "crux" or "heart" of Linear Algebra and that the understanding of it is crucial for further study.

But what I don't understand is WHY? Why are they so important?

I understand that :

• Row Space and Null Space are orthogonal. (Same for other two)
• Their dimensions are governed by rank of the matrix.

but beyond that I didn't find anything that I found profound or interesting. Am I missing something or is Prof. Strang over-rating the 4 fundamental subspaces?

Answer 1

The core of studying matrices is to study linear transformations between vector spaces. These can be realized as matrix multiplication on the left (or right) of column (or row) vectors.

If we are in this setup: $x\mapsto Ax$ for a column vector $x$ and appropriate matrix $A$, then the image of the linear transformation will be spanned by the columns of $A$.

The kernel of the transformation (nullspace) is the set of all $x$ such that $Ax=0$ is important for understanding the solutions to some matrix equations. You probably have already learned that if $x_0$ is a solution to $Ax=b$, then every other solution is given by $x_0+k$ where $k$ is in the nullspace.

This all has analogous explanation on the other side. If we are in this setup: $x\mapsto xA$ for a row vector $x$, then the image of the linear transformation is now spanned by the rows of $A$.

Talking about the nullspace of $A^T$ is just a fancy way of dressing up the "left nullspace" of $A$, since $xA=0$ iff $A^T x^T=0$. The nullspace is now the set of all $x$ such that $xA=0$, and you can draw the same conclusions about solutions to $xA=b$.

In short, these four spaces (really just two spaces, with a left and a right version of the pair) carry all the information about the image and kernel of the linear transformation that $A$ is affecting, whether you are using it on the right or on the left.

Answer 2

Consider a linear map ${ A : \mathbb{R} ^n \longrightarrow \mathbb{R} ^m . }$ Consider its adjoint ${ A ^T : \mathbb{R} ^m \longrightarrow \mathbb{R} ^n . }$

Note that in ${ \mathbb{R} ^n }$ the maps give subspaces ${ \text{ker}(A) }$ and ${ \text{im}(A ^T) . }$

Note that ${ \text{im}(A ^T) \subseteq \text{ker}(A) ^{\perp} . }$

Let ${ x \in \text{im}(A ^T) . }$ We are to show $${ \text{To show: } \quad x ^T y = 0 \quad \text{ for all } y \in \text{ker}(A) . }$$ Note that ${ x = A ^T x _0 . }$ Let ${ y \in \text{ker}(A) . }$ Then note that ${ x ^T y }$ ${ = x _0 ^T A y = 0 , }$ as needed.

Note that ${ \text{im}(A ^T) }$ and ${ \text{ker}(A) ^{\perp} }$ have the same dimension.

Hence

$${ \text{im}(A ^T) = \text{ker}(A) ^{\perp} . }$$

Note that replacing ${ A }$ with ${ A ^T }$ we have

$${ \text{im}(A) = \text{ker}(A ^T) ^{\perp} . }$$

Hence the action of ${ A }$ and ${ A ^T }$ is given by

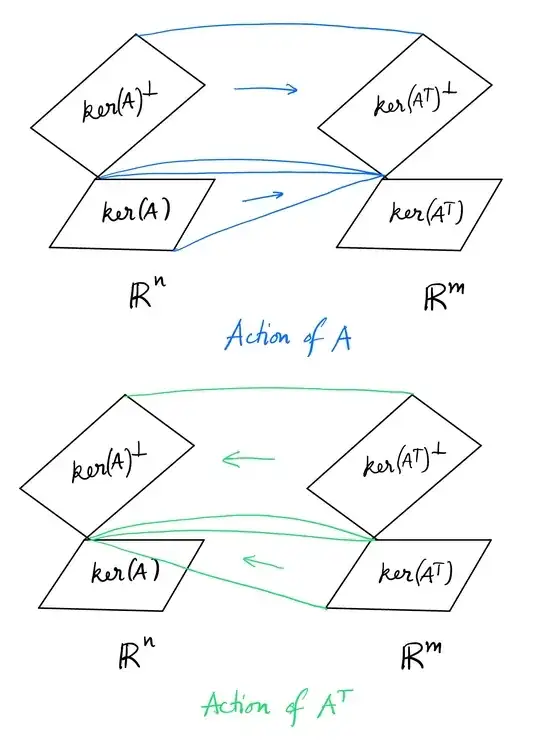
Note that the images ${ {\color{blue}{\text{im}(A)}} }$ and ${ {\color{green}{\text{im}(A ^T)}} }$ are effectively the ${ {\color{blue}{\text{column space}}} }$ and ${ {\color{green}{\text{row space}}} }$ of ${ A }$ respectively.

---

Here are some example observations from the above “4 fundamental subspaces” picture:

Note that ${ \mathcal{N}(A ^T A) = \mathcal{N}(A) }$.

Note that ${ \mathcal{R}(A ^T A) = \mathcal{R}(A ^T) }$. (Alt proof: The inclusion ${ \subseteq }$ is clear. Then from a dimension argument we get equality).

Note that roughly speaking, every linear map ${ A }$ sends its row space to its column space. (The only interesting images ${ Ax }$ are when the inputs ${ x }$ are in the row space of ${ A }$).

Note that if we append orthonormal bases of null space of ${ A }$ and row space of ${ A }$ (note that these can be computed by row reduction and Gram-Schmidt process) we get a good orthonormal basis of the domain.

And so on.