Stronger than Nesbitt inequality

Question

For $x,y,z >0$, prove that $$\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} \geqslant \sqrt{\frac94+\frac32 \cdot \frac{(y-z)^2}{xy+yz+zx}}$$

Observation:

1. This inequality is stronger than the famous Nesbitt's Inequality $$\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} \geqslant \frac32 $$ for positive $x,y,z$
2. We have three variables but the symmetry holds only for two variables $y,z$, resulting in a very difficult inequality. Brute force and Largrange Multiplier are too complicated.
3. The constant $\frac32$ is closed to the best constant. Thus, this inequality is very sharp, simple AM-GM estimation did not work.

Update: As point out by Michael Rozenberg, this inequality is still unsolved

Answer 1

Here's a proof.

Using Lagrange's identity leads to $$\sum_{cyc}\frac{x}{y+z}=\frac32+\frac12\sum_{cyc}\frac{(x-y)^2}{(x+z)(y+z)} \qquad (*)$$

We get this by letting $a = \sqrt{x+y}$, $b = \sqrt{y+z}$, $c = \sqrt{z+x}$, $d = \frac{1}{\sqrt{x+y}}$, $e = \frac{1}{\sqrt{y+z}}$, $f = \frac{1}{\sqrt{z+x}}$, and by Lagrange's identity, $$(a^2+b^2+c^2)(d^2+e^2+f^2) = (ad+be+cf)^2 + (ae-bd)^2+(af-cd)^2+(bf-ce)^2$$ which gives $$2 (x+y+z)(\sum_{cyc}\frac{1}{y+z}) = 9 + \sum_{cyc} \left(\frac{\sqrt{x+y}}{\sqrt{y+z}} - \frac{\sqrt{y+z}}{\sqrt{x+y}}\right)^2$$ or $$3 +\sum_{cyc}\frac{x}{y+z} = \frac92 + \frac12\sum_{cyc} \frac{\left({x+y} - (y+z)\right)^2}{({y+z})(x+y)} $$ which is the desired equation $(*)$.

Squaring both sides of the inequality then gives

$$ \tag{1} \frac16 \left[ \sum_{cyc}\frac{(x-y)^2}{(x+z)(y+z)} \right ]^2 + \sum_{cyc}\frac{(x-y)^2}{(x+z)(y+z)} \geq \frac{(y-z)^2}{xy + yz + xz} $$

We will follow two paths for separate cases.

Path 1: Omitting the square term it suffices to prove $$\sum_{cyc}\frac{(x-y)^2}{(x+z)(y+z)} \geqslant \frac{(y-z)^2}{xy + yz + xz}$$

Clearing denominators, we obtain $$ (x-y)^2 (x+y) + (y-z)^2 (y+z) + (z-x)^2 (z+x) \geq \frac{(y-z)^2}{xy + yz + xz} (x+y) (y+z) (z+x) $$

Using $(x+y)(y+z)(x+z) = (x+y+z)(xy + yz+ xz) - x y z$ it suffices to show

$$ (x-y)^2 (x+y) + (y-z)^2 (y+z) + (z-x)^2 (z+x) \geq {(y-z)^2} (x+y+z) $$ or $$ (x-y)^2 (x+y) + (z-x)^2 (z+x) \geq (y-z)^2 x $$

Since $$ (y-z)^2 = (y-x + x- z)^2 = (y-x)^2 + (x- z)^2 + 2 (y-x)(x-z) $$ this translates into

$$ (y-x)^2 y + (x-z)^2 z \geq 2 x(y-x)(x-z) $$ For the two cases $y\geq x ; z\geq x $ and $y\leq x ; z\leq x $ the RHS $\leq 0$ so we are done. For the other two cases, by symmetry, it remains to show the case $y> x ; z < x $.

Rearranging terms, we can also write $$ (y-x)^3 - (x-z)^3 +x ((y - x) + (z-x))^2 \geq 0 $$

This holds true at least for $(y-x)^3 \geq (x-z)^3$ or $y+z\geq 2 x$.

So the proof is complete other than for the case $y+z < 2x$ and [ $y> x ; z < x $ or $z> x ; y < x $ ].

Path 2.

For the remaining case $y+z < 2 x $ and [$y> x ; z < x$ or $z> x ; y < x $] we will follow a different path. Again, by symmetry, we must inspect only $y+z < 2x$ and $y> x > z$.

A remark up front: In the following, some high order polynomials of one variable have to be inspected. MATLAB is used, also for plotting behaviours of these polynomials. There is no case in spending effort for further analytical work on polynomials where their behaviour is obvious. Still, what follows contains some "ugly" parts.

In the squared version (1) of the inequality, we can use a further inequality which has been proved here: $$\sum_{cyc}\frac{(x-y)^2}{(x+z)(y+z)} \geqslant \frac{27}{8} \frac{(y-z)^2}{(x+y+z)^2}$$

So it suffices to prove

$$ \frac16 \left[ \frac{27}{8} \frac{(y-z)^2}{(x+y+z)^2} \right ]^2 + \sum_{cyc}\frac{(x-y)^2}{(x+z)(y+z)} \geq \frac{(y-z)^2}{xy + yz + xz} $$

Some numerical inspection shows immediately that the first term cannot be ommitted.

Clearing some denominators gives

$$ \tag{2} \frac16 \left[ \frac{27}{8} \right ]^2 \frac{(y-z)^4 (xy + yz + xz) (x+y)(y+z) (z+x)}{(x+y+z)^4} + \\ (xy + yz + xz) \sum_{cyc} {(x-y)^2}{(x+y)} - (y-z)^2 (x+y)(y+z) (z+x) \geqslant 0 \quad $$

By homogeneity, we set $y=1+z$.

The condition $y+z < 2x$ then translates into $1+2z < 2x$, hence we further set $x = z + (1 +q)/2$ where $0\leq q \leq 1$ since also $x = z + (1 +q)/2 < y = 1 +z$.

Inserting $y=1+z$ and $x = z + (1 +q)/2$ into (2) is straightforward, the result is lengthy (not displayed here).

Let us start with focussing on the first term in (2), calling that fraction $F$: $$ F= \frac{(y-z)^4 (xy + yz + xz) (x+y)(y+z) (z+x)}{(x+y+z)^4} $$ With the setting $y=1+z$ this can be simplified to $$ F = \frac{(xy + yz + xz) (x+y)(y+z) (z+x)}{(x+y+z)^4} $$

Since by the settings $y=1+z$ and $x = z + (1 +q)/2$ both x and y are linear in z, the numerator of $F$ is of fifth order in $z$, whereas the denominator is of fourth order in $z$. In leading order, the whole term is therefore of first order in $z$ and will therefore rise with $z$ for large enough $z$. This motivates to show that indeed $$F(q,z) \geq F(q,z=0) = 2 \frac{(q+1)^2}{(q+3)^2}$$ for all $z$ and $q$. Showing that directly requires a condition

$$ G = (xy + yz + xz) (x+y)(y+z) (z+x) (q+3)^2 - 2 (q+1)^2 (x+y+z)^4 \geq 0 $$

Inserting $y=1+z$ and $x = z + (1 +q)/2$ into $G$, and expanding the brackets, gives a very lengthy expression which however contains only positive terms, so the condition is proved immediately:

$$ G = (z(2q^6z + 2q^6 + 22q^5z^2 + 51q^5z + 22q^5 + 80q^4z^3 + 358q^4z^2 + 357q^4z + 100q^4 + 96q^3z^4 + 960q^3z^3 + 1828q^3z^2 + 1206q^3z + 260q^3 + 864q^2z^4 + 3672q^2z^3 + 4788q^2z^2 + 2484q^2z + 450q^2 + 2592qz^4 + 7344qz^3 + 7398qz^2 + 3159qz + 486q + 2592z^4 + 5832z^3 + 4806z^2 + 1701z + 216))/4 \geq 0 $$

Hence it suffices, instead of (2), to prove the following:

$$ \tag{3} \frac16 \left[ \frac{27}{8} \right ]^2 2 \frac{(q+1)^2}{(q+3)^2} + (xy + yz + xz) \sum_{cyc} {(x-y)^2}{(x+y)} \\ - (x+y)(y+z) (z+x) \geqslant 0 \quad $$

After insertion of $y=1+z$ and $x = z + (1 +q)/2$, the factors $(x-y)^2$ in the cyclic sum will not be functions of $z$. Hence, the LHS is a third order expression in $z$ with leading (in $z^3$ ) term $( 1 + 3 q^2) z^3$, so for large enough $z$ it is rising with $z$. A remarkable feature of this expression is that for the considered range $0\leq q \leq 1$ it is actually monotonously rising for all $z$. To see this, consider whether there are points with zero slope. The first derivative of the expression with respect to $z$ is

$$ q^4/4 + (7q^3z)/2 + (7q^3)/4 + 9q^2z^2 + 9q^2z + (5q^2)/4 - (7qz)/2 - (7q)/4 + 3z^2 + 3z + 1/2 $$ Equating this to zero gives $$ z_{1} = -(2((13q^6)/4 + (17q^4)/2 + (133q^2)/4 + 3)^{(1/2)} - 7q + 18q^2 + 7q^3 + 6)/(36q^2 + 12)\\ z_{2} = -(-2((13q^6)/4 + (17q^4)/2 + (133q^2)/4 + 3)^{(1/2)} - 7q + 18q^2 + 7q^3 + 6)/(36q^2 + 12) $$ One now shows that in the range $0\leq q \leq 1$, there are only negative solutions $z_{1,2}$. So we will have no zero slopes for $z\geq 0$. Since the polynomials are (roots of) sixth order in q, we investigate the following figures:

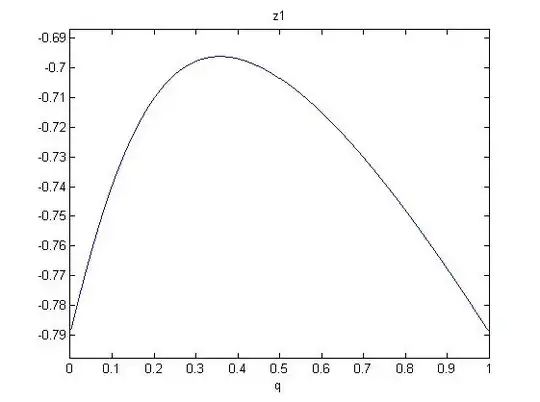
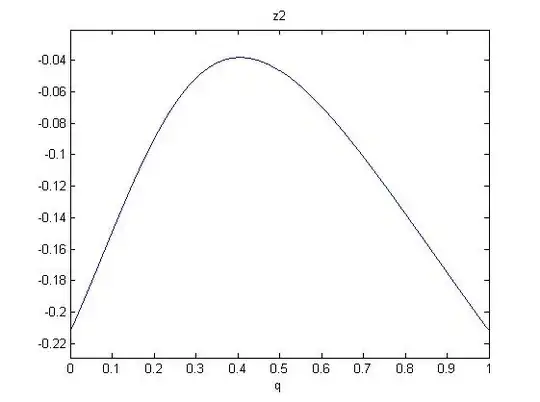
So monotonicity (rising with $z$) is established for all $q$.

Hence, to show the inequality it suffices to inspect (3) at the smallest $z=0$. This gives

$$ ((q + 1)(8q^6 + 88q^5 + 336q^4 + 432q^3 - 216q^2 - 405q + 243))/(64(q + 3)^3) \geqslant 0 \quad $$ or

$$ \tag{4} 8q^6 + 88q^5 + 336q^4 + 432q^3 - 216q^2 - 405q + 243 \geqslant 0 \quad $$

An even stronger requirement is $$ h(q) = 432q^3 - 216q^2 - 405q + 243 \geq 0 $$ In the considered range $0\leq q \leq 1$, $h(q)$ has a minimum which is obtained by taking the first derivative, $$ 1296 q^2 - 432 q - 405 $$ and equating to zero, which gives $q = 3/4$, and the above $h(q)$ then gives $$ h(q = 3/4) = 0 $$

This establishes the inequality. $ \qquad \Box$

Answer 2

Since our inequality is symmetric on $y$ and $z$ , we need to check two cases:

1. $x=\min\{x,y,z\}$.

Let $y=x+u$ and $z=x+v$. Hence, $$4\prod_{cyc}(x+y)^2(xy+xz+yz)\left(\left(\sum\limits_{cyc}\frac{x}{y+z}\right)^2-\frac{9}{4}-\frac{3(y-z)^2}{2(xy+xz+yz)}\right)=$$ $$=192(u^2+uv+v^2)x^6+48(10u^3+13u^2v+13uv^2+10v^3)x^5+$$ $$+48(10u^4+17u^3v+18u^2v^2+17uv^3+10v^4)x^4+$$ $$+4(62u^5+133u^4v+158u^3v^2+158u^2v^3+133uv^4+62v^5)x^3+$$ $$+(68u^6+192u^5v+225u^2v^4+298u^3v^3+225u^2v^4+192uv^5+68v^6)x^2+$$ $$+(8u^7+40u^6v+34u^5v^2+66u^4v^3+66u^3v^4+34u^2v^5+40uv^6+8u^7)x+$$ $$+uv(u+v)^2(4u^4-6u^3v+11u^2v^2-6uv^3+4v^4)\geq0;$$ 2. $x\neq\min\{x,y,z\}$.

Let $x=y+u$ and $z=y+v$. Hence, $$4\prod_{cyc}(x+y)^2(xy+xz+yz)\left(\left(\sum\limits_{cyc}\frac{x}{y+z}\right)^2-\frac{9}{4}-\frac{3(y-z)^2}{2(xy+xz+yz)}\right)=$$ $$=192(3u^2-3uv+v^2)y^6+48(26u^3-3u^2v-19uv^2+10v^3)y^5+$$ $$+48(22u^4+21u^3v-26u^2v^2-7uv^3+10v^4)y^4+$$ $$+4(110u^5+253u^4v-58u^3v^2-226u^2v^3+37uv^4+62v^5)y^3+$$ $$+(92u^6+384u^5v+201u^2v^4-374u^3v^3-231u^2v^4+144uv^5+68v^6)y^2+$$ $$+2(4u^7+32u^6v+41u^5v^2-15u^4v^3-51u^3v^4-7u^2v^5+20uv^6+4u^7)y+$$ $$+uv(u+v)^2(4u^4-u^2v^2-6uv^3+4v^4)\geq0.$$ Done!

For example, $$4u^4-u^2v^2-6uv^3+4v^4=(2u^2-v^2)^2+3(u-v)^2\geq0;$$ Also, by AM-GM $$4u^7+32u^6v+41u^5v^2-15u^4v^3-51u^3v^4-7u^2v^5+20uv^6+4u^7=$$ $$=(u+v)(4u^6+28u^5v+13u^4v^2-28u^3v^3-23u^2v^4+16uv^5+4v^6)=$$ $$=(u+v)((2u^3+7u^2v-9uv^2+v^3)^2+(94u^3-118u^2v+34uv^2+3v^3)v^3)\geq$$ $$\geq v^3(u+v)(94u^3-118u^2v+34uv^2+3v^3)=$$ $$=v^3(u+v)\left(9\cdot\frac{94}{9}u^3+7\cdot\frac{34}{7}uv^2+3v^3-118u^2v\right)\geq$$ $$\geq v^3(u+v)\left(17\sqrt[17]{\left(\frac{94}{9}\right)^9\left(\frac{34}{7}\right)^7\cdot3}-118\right)u^2v\geq0.$$

Answer 3

Alternative solution: (with the help of computer)

WLOG, assume $z = 1$. Let $p = x + y, q = xy$. The desired inequality is written as $$\frac{p + p^2 - 2q}{1 + p + q} + \frac{1}{p} \ge \sqrt{\frac94 + \frac32 \frac{p^2 - 4q}{p + q}}.$$ We have \begin{align*} &\left(\frac{p + p^2 - 2q}{1 + p + q} + \frac{1}{p}\right)^2 - \left(\frac94 + \frac32 \frac{p^2 - 4q}{p + q}\right)\\ =\ & \frac{q^3}{4(p + q)(1 + p + q)^2p^7}(c_3Q^3 + c_2Q^2 + c_1Q + c_0) \end{align*} where \begin{align*} Q &= \frac{p^2 - 4q}{4q}, \\ c_3 &= 256\,{p}^{6}+128\,{p}^{5}-576\,{p}^{4}-512\,{p}^{3}+192\,{p}^{2}+512\,p+256 , \\ c_2 &= 64\,{p}^{7}+448\,{p}^{6}+208\,{p}^{5}-1408\,{p}^{4}-1232\,{p}^{3}+832 \,{p}^{2}+1600\,p+768, \\ c_1 &= 40\,{p}^{7}+244\,{p}^{6}+56\,{p}^{5}-1104\,{p}^{4}-896\,{p}^{3}+1088\, {p}^{2}+1664\,p+768, \\ c_0 &= 7\,{p}^{7}+36\,{p}^{6}-20\,{p}^{5}-272\,{p}^{4}-176\,{p}^{3}+448\,{p}^ {2}+576\,p+256. \end{align*} Clearly, $Q \ge 0$. We can prove that $c_3, c_2, c_1, c_0\ge 0$ for all $p\ge 0$.

We are done.

Answer 4

Partial answer.

Lemma 1 :

$a,b,c>0$ then we have :

$$\sum_{cyc}\frac{a}{b+c}\geq P(a,b,c)=\sqrt{\frac{9}{4}+\frac{9}{4}\frac{(c^4+a^4+b^4-c^2a^2-b^2a^2-c^2b^2)}{((a+b+c)\frac{3}{4}+\frac{3}{4}(abc)^{\frac{1}{3}})(a+b)(b+c)(c+a)}+\frac{(c^2+a^2+b^2-ca-ba-cb)(a+b+c)}{(a+b)(b+c)(c+a)}}$$

Proof of lemma 1 :

First we remark that the inequality is homogenous and we can try the substitution $3u=a+b+c$, $3v^2=ab+bc+ca$ and $w^3=abc$ and apply the uvw's method .

We have : $$a^4+b^4+c^4=(9u^2-6v^2)^2-2(9v^4-6uw^3)$$ $$a^2b^2+b^2c^2+c^2a^2=9v^4-6uw^3$$ $$a^2+b^2+c^2=9u^2-6v^2$$

And : $\left(\frac{((3u)((3u)^2-4(3v^2))+5w^3)}{3u3v^2-w^3}+2\right)^2\geq \frac{9}{4}+\frac{(9/4)((9u^2-6v^2)^2-2(9v^4-6uw^3)-(9v^4-6uw^3))+(2.25u+0.75w)(9u^2-9v^2)(3u)}{(2.25u+0.75w)(3u3v^2-w^3)}$

it's enough to find an extreme value of our expression for the extreme value of $w^3$ wich happens for an equality case of two variables .

Since the last inequality is homogeneous, we can assume that $b=c=1$.

$$\frac{2}{a+1}+\frac{a}{2}\geq\sqrt{\frac{9}{4}+\frac{9}{4}\frac{(a^4+1-2a^2)}{((a+2)\frac{3}{4}+\frac{3}{4}(a)^{\frac{1}{3}})(a+1)^2(2)}+\frac{(a^2+1-2a)(a+2)}{(a+1)^2(2)}}$$

Now it seems to be clear : we get a polynomial with a root equal to one . See the factorization by Wolfram alpha .

End of the proof of the lemma 1

With the assumption (wich makes the partial answer) $1\geq a\geq b \geq c>0$ $$P(a,b,c)\geq \sqrt{\frac94+\frac32 \cdot \frac{(a-b)^2}{ab+bc+ca}}$$

To prove it we have :

$$P(a,b,c)\geq\sqrt{\frac{9}{4}+\frac{3}{2}\frac{(a-b)^2(a+b+c)}{(a+b)(b+c)(c+a)}}\geq \sqrt{\frac94+\frac32 \cdot \frac{(a-b)^2}{ab+bc+ca}}$$

Wich is really smooth (proving the inequality term by term or fraction by fraction).Conclude using the lemma 1.

For the other case it's true with the assumption $a\geq c \geq b \geq \frac{a}{9}$ but currently I cannot prove it !

Update 14/04/2021 :

Conjecture :

Let $a,b,c>0$ then we have :

$$\sum_{cyc}\frac{a}{b+c}\geq\sqrt{\frac{9}{4}+\frac{9}{4}\frac{(c^4+a^4+b^4-c^2a^2-b^2a^2-c^2b^2)}{(0.75(abc)^{\frac{1}{3}}+0.75(a+b+c))(a+b)(b+c)(c+a)}+\frac{(c^2+a^2+b^2-ca-ba-cb)(a+b+c)}{(a+b)(b+c)(c+a)}+4\left(abc\frac{\left(\frac{a^2+b^2+c^2}{ab+bc+ca}-1\right)^4}{a^3+b^3+c^3}\right)}\geq\sqrt{\frac{9}{4}+\frac{3}{2}\frac{(a-b)^2}{ab+bc+ca}}$$

Update 16/04/2021 :

For the LHS I think we can use the uvw's method or Buffalo's way using a computer (I'm not againt the "computer-proof" if you want to know).The problem is :if we use the Tej's theorem it's sufficient to show a symmetric inequality when $a=b=1$ with a degree less than $5$ wich is not the case here .In the case where Tej's theorem works we have the following factorization by WA .See also the reference On the Abstract Concreteness Method (bka $ABC-$Method). .

It seems that we have the following inequalities :

Let $a,b,c>0$ :

$$\frac{(c^2+a^2+b^2-ca-ba-cb)(a+b+c)}{(a+b)(b+c)(c+a)}\geq \frac{3}{4}\frac{(a-b)^2}{ab+bc+ca}$$

$a,b,c\in[0.5,1]$

$$\frac{9}{4}\frac{(c^4+a^4+b^4-c^2a^2-b^2a^2-c^2b^2)}{(\frac{3}{4}(abc)^{\frac{1}{3}}+\frac{3}{4}(a+b+c))(a+b)(b+c)(c+a)}\geq \frac{3}{4}\frac{(a-b)^2}{ab+bc+ca}$$

$a,b,c\in[0.2,1]$ then we have :

$$\frac{9}{4}\frac{(c^{4}+a^{4}+b^{4}-c^{2}a^{2}-b^{2}a^{2}-c^{2}b^{2})}{(0.75(abc)^{\frac{1}{3}}+0.75(a+b+c))(a+b)(b+c)(c+a)}+8\left(abc\frac{\left(\frac{a^{2}+b^{2}+c^{2}}{ab+bc+ca}-1\right)^{4}}{a^{3}+b^{3}+c^{3}}\right)-\frac{3}{4}\frac{(a-b)^{2}}{ab+bc+ca}\geq 0$$ And

$$\frac{(c^{2}+a^{2}+b^{2}-ca-ba-cb)(a+b+c)}{(a+b)(b+c)(c+a)}-\frac{3}{4}\frac{(a-b)^{2}}{ab+bc+ca}-4\left(abc\frac{\left(\frac{a^{2}+b^{2}+c^{2}}{ab+bc+ca}-1\right)^{4}}{a^{3}+b^{3}+c^{3}}\right)\geq 0$$

Answer 5

Abstract :

We suggests a way to show the OP inequality so some part are left to the reader because there are easy . We spilt the problem in two cases , first case $2c-2b\le a$ and the second $2c-2b\ge a$ . As the problem is homogenous we suppose in addition $1\ge a\ge c\ge b$.Following that we use convexity and derivatives.

---

First case : $1\ge a\ge c\ge b$ and $2c-2b\le a$

we have :

$$\sum_{cyc}\frac{a}{b+c}\geq 1.5+0.5\frac{(a-b)^2}{ab+bc+ca}\geq \sqrt{\frac{9}{4}+1.5\frac{(a-b)^2}{ab+bc+ca}}$$

Or:

$$\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}-1.5\right)\left(ab+bc+ca\right)-\frac{\left(a-b\right)^{2}}{2}\geq 0\quad (C)$$

---

SubCase : $a\ge 2c\ge c\ge b$

$$\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}-1.5\right)\left(ab+bc+ca\right)\geq \frac{2(a^2+b^2+c^2-ab-bc-ca)}{3}\geq\frac{\left(a-b\right)^{2}}{2}\quad $$

Wich is trivial using the $uvw's$ method and the assumptions on $a,b,c>0$

---

Subcase: $2c\geq a \geq c\geq b$ and $c+b\leq a $ and $a\geq 2c-2b$ remarking that :

$$f(c)=\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}-1.5\right)\left(ab+bc+ca\right)$$

Is a decreasing function always with the assumptions above .Remains to show the cases $a=c+b$ or $a=2c-2b$ wich is a one variable inequality since all the equalities/inequalities are homogenous.I shall prove that the function is decreasing later .

To prove that the function is decreasing we differentiate twice we have :

$$f''(c)=-\frac{2a^2b}{(a+c)^3}-\frac{2ab^2}{(b+c)^3 }+2$$

With the assumptions above the function $f(c)$ is convex so the derivative is increasing .Remains to show the inequality at the equality case wich is not hard .

---

Second case: $1\ge a\geq c\geq b>0$ and $2c-2b\ge a$

$$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge 1.5+\frac{\left(\sqrt{\frac{15}{4}}-1.5\right)\left(\left|a-b\right|\right)^{1.75}}{\left(ab+bc+ca\right)^{\frac{1.75}{2}}}\geq \sqrt{\frac{9}{4}+1.5\frac{(a-b)^2}{ab+bc+ca}} $$

To prove it we remark :

$$f(c)=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}-1.5$$

Is increasing with $a\leq 2c-2b$ as $f(c)$ is a convex function we deduce that the first derivative is increasing . Remains to replace by the constraint $2c-2b=a$

$$g(c)=\left(ab+bc+ca\right)^{\frac{1.75}{2}}$$

Is increasing .

So the product of two positives increasing functions is also an increasing function always with constraints above .

It remains to show the case $a=2c-2b$ . As it's homogenous we get an inequality with one variable or a long polynomial .The RHS is trivial .

Last Edit 09/03/2022 :

We have the inequality :

Let $0\leq x\leq 1$ then we have :

$$\sqrt{\frac{9}{4}+1.5x}\leq g(x)=\left(2-a\right)\frac{1}{2}\sqrt{\frac{3}{5}}\left(ax-a\right)+\sqrt{\frac{9}{4}+1.5}+\frac{-\sqrt{\frac{3}{5}}}{20}\left(a^{-1}x-a^{-1}\right)^{2}$$

Where $a\geq 0$ is chosen as :

$$g(0)=1.5$$

We can do really better as it seems we have for $0\leq x\leq 1$ :

$$\left(2-a^{1.0735}\right)\frac{1}{2}\sqrt{\frac{3}{5}}\left(ax-a\right)+\sqrt{\frac{9}{4}+1.5}+\frac{-\sqrt{\frac{3}{5}}}{20}\left(a^{-1}x-a^{-1}\right)^{2}\geq \sqrt{\frac{9}{4}+1.5x}$$

Where $a\simeq 0.7748951014$ is chosen as :

$$g(0)=1.5$$